题目内容
2．设A=2a2-a，B=-a2-a，求：（1）A+B．
（2）A-B．
分析 （1）根据A=2a2-a，B=-a2-a，直接代入A+B计算即可；
（2）根据A=2a2-a，B=-a2-a，直接代入A-B计算即可．
解答 解：（1）∵A=2a2-a，B=-a2-a，
∴A+B=（2a2-a）+（-a2-a）
=a2-2a；
（2）∵A=2a2-a，B=-a2-a，
∴A-B=（2a2-a）-（-a2-a）
=3a2．
点评 本题考查了整式的加减，掌握去括号与合并同类项的法则是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．
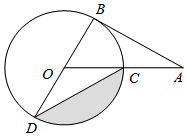如图，AB为⊙O的切线，切点为B，连接AO，OA与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为4，则图中阴影部分的面积为（ ）
如图，AB为⊙O的切线，切点为B，连接AO，OA与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为4，则图中阴影部分的面积为（ ）| A． | $\frac{4}{3}π-\sqrt{3}$ | B． | $\frac{4}{3}π-2\sqrt{3}$ | C． | $4π-4\sqrt{3}$ | D． | $\frac{16}{3}π-4\sqrt{3}$ |
如图，点O为 Rt△ABC斜边AB上的一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD．
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．
17．下列各式中，没有意义的是（ ）
| A． | $\sqrt{\frac{1}{4}}$ | B． | $\sqrt{（-2）^{2}}$ | C． | $\sqrt{-\frac{1}{3}}$ | D． | $-\sqrt{2}$ |
7．下列各式中，属于二次根式的有（ ）
①$\sqrt{15}$；②$\sqrt{\frac{1}{a}}$；③$\sqrt{{a}^{2}+{b}^{2}}$；④$\sqrt{{a}^{2}b}$；⑤$\sqrt{2ab×3bc}$；⑥$\sqrt{5\frac{1}{2}}$．
①$\sqrt{15}$；②$\sqrt{\frac{1}{a}}$；③$\sqrt{{a}^{2}+{b}^{2}}$；④$\sqrt{{a}^{2}b}$；⑤$\sqrt{2ab×3bc}$；⑥$\sqrt{5\frac{1}{2}}$．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
11．（π-3）0+2-2=（ ）
| A． | 5 | B． | 1$\frac{1}{4}$ | C． | -3 | D． | -1$\frac{1}{4}$ |
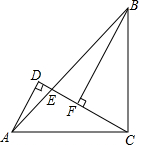如图所示，△ADC是直角三角形，∠ADC=90°，AC=BC，且AC⊥BC于点C，BF⊥CD于F，连接AB交CD于E，试说明：AD+DF=BF．