题目内容
1.已知抛物线y=x2+bx+c经过点(1,-4)和(-1,2),求这个抛物线的顶点坐标.分析 利用待定系数法即可求出二次函数解析式,配方成抛物线的顶点式即可求出抛物线的顶点坐标.
解答 解:(1)把点(1,-4)和(-1,2)代入y=x2+bx+c,得$\left\{\begin{array}{l}{1+b+c=-4}\\{1-b+c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-3}\\{c=-2}\end{array}\right.$,所以抛物线的解析式为y=x2-3x-2.
y=x2-3x-2=(x-$\frac{3}{2}$)2-$\frac{17}{4}$,
所以抛物线的顶点坐标为($\frac{3}{2}$,-$\frac{17}{4}$).
点评 本题主要考查了用待定系数法求二次函数解析式及二次函数的性质,解题的关键是正确求出二次函数的解析式.

练习册系列答案
相关题目
12.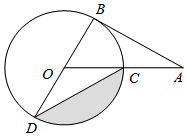 如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
 如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )| A. | $\frac{4}{3}π-\sqrt{3}$ | B. | $\frac{4}{3}π-2\sqrt{3}$ | C. | $4π-4\sqrt{3}$ | D. | $\frac{16}{3}π-4\sqrt{3}$ |
11.(π-3)0+2-2=( )
| A. | 5 | B. | 1$\frac{1}{4}$ | C. | -3 | D. | -1$\frac{1}{4}$ |
 如图,点O为 Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,点O为 Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.