题目内容
16.在学习因式分解时,我们学习了“提公因式法”和“公式法”,事实上,除了这两种方法外,还有其它方法可以用来因式分解,比如配方法.例如,如果要因式分解x2+2x-3时,显然既无法用提公因式法,也无法用公式法,怎么办呢?这时,我们可以采用下面的办法:x2+2x-3=x2+2•x•1+12-1-3------①
=(x+1)2-22------②
=(x+1+2)(x+1-2);
=(x+3)(x-1).
解决下列问题:
(1)填空:在上述材料中,运用了转化(选填一项:“分类、转化、数形结合、方程”)的思想方法,使得原题变为可以继续用平方差公式因式分解,这种方法就是配方法;
(2)显然所给材料中因式分解并未结束,请在横线上继续完成因式分解过程;
(3)请用上述方法因式分解x2-4x-5.
分析 (1)上述材料中运用了转化的数学思想;
(2)在横线上继续完成因式分解过程即可;
(3)利用上述方法将原式分解即可.
解答 解:x2+2x-3=x2+2•x•1+12-1-3------①
=(x+1)2-22------②
=(x+1+2)(x+1-2)
=(x+3)(x-1).
(1)在上述材料中,运用了转化的思想方法,使得原题变为可以继续用平方差公式因式分解,这种方法就是配方法,
故答案为:转化;
(2)故答案为:(x+1+2)(x+1-2);(x+3)(x-1);
(3)原式=x2-4x+4-4-5=(x-2)2-9=(x-2+3)(x-2-3)=(x+1)(x-5).
点评 此题考查了因式分解-十字相乘法,弄清题中的解题方法是解本题的关键.

练习册系列答案
相关题目
6.解下列不等式组,结果正确的是( )
| A. | 不等式组$\left\{{\begin{array}{l}{x>7}\\{x>3}\end{array}}\right.$的解集是x>3 | |
| B. | 不等式组$\left\{{\begin{array}{l}{x<-3}\\{x>-2}\end{array}}\right.$的解集是-3<x<-2 | |
| C. | 不等式组$\left\{{\begin{array}{l}{x<-3}\\{x<-1}\end{array}}\right.$的解集是x<-1 | |
| D. | 不等式组$\left\{{\begin{array}{l}{x>-4}\\{x<2}\end{array}}\right.$的解集是-4<x<2 |
8.解分式方程$\frac{2}{x+1}+\frac{3}{x-1}=\frac{6}{{{x^2}-1}}$,分以下四步,其中,错误的一步是( )
| A. | 方程两边分式的最简公分母是(x-1)(x+1) | |
| B. | 方程两边都乘以(x-1)(x+1),得整式方程2(x-1)+3(x+1)=6 | |
| C. | 解这个整式方程,得x=1 | |
| D. | 原方程的解为x=1 |
5.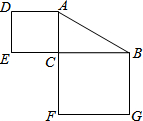 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )| A. | 225 | B. | 200 | C. | 250 | D. | 150 |
6.在计算结果为a6的个数是( )
| A. | a2•a3 | B. | a12÷a2 | C. | (-a2)3 | D. | a4•a2 |
 如图,矩形ABCD两条对角线相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长是4.
如图,矩形ABCD两条对角线相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长是4. 如图,若AB∥CD,CE平分∠DCB,且∠B+∠DAB=180°.证明:∠E=∠3.
如图,若AB∥CD,CE平分∠DCB,且∠B+∠DAB=180°.证明:∠E=∠3.