题目内容
15.化简:$\frac{1}{x(x+m)}+\frac{1}{(x+m)(x+2m)}+\frac{1}{(x+2m)(x+3m)}+…$$+\frac{1}{[x+(n-1)m](x+nm)}$.分析 根据题意找出规律进行计算即可.
解答 解:原式=$\frac{1}{m}$($\frac{1}{x}$-$\frac{1}{x+m}$+$\frac{1}{x+m}$-$\frac{1}{x+2m}$+…+$\frac{1}{x+(n-1)m}$-$\frac{1}{x+mn}$)
=$\frac{1}{m}$($\frac{1}{x}$-$\frac{1}{x+mn}$)
=$\frac{1}{m}$•$\frac{mn}{x(x+mn)}$
=$\frac{n}{x(x+mn)}$.
点评 本题考查的是分式的加减法,根据题意找出规律是解答此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
3.若二次函数y=ax2+c(a≠0)的图象上有两点(x1,5),(x2,5),且x1≠x2,则当x取x1+x2时,函数值为( )
| A. | a+c | B. | a-c | C. | -c | D. | c |
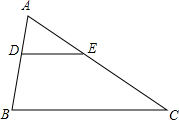 如图,点D,E分别在AB,AC上,DE∥BC,若AD:BD=2:3,BC=15cm,求DE的长.
如图,点D,E分别在AB,AC上,DE∥BC,若AD:BD=2:3,BC=15cm,求DE的长. 如图是一名学生推铅球时,铅球运行高度y(m)与水平距离x(m)之间的函数图象,铅球推出4m时达到最高点,最高点到地面的距离为3m,铅球推出时高度为1.5m,则铅球推出的最大距离为9.7m.(结果精确到0.1米)
如图是一名学生推铅球时,铅球运行高度y(m)与水平距离x(m)之间的函数图象,铅球推出4m时达到最高点,最高点到地面的距离为3m,铅球推出时高度为1.5m,则铅球推出的最大距离为9.7m.(结果精确到0.1米)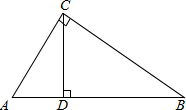 如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.