题目内容
5．设△ABC三边为a、b、c，其中a、b满足|a+b-6|+（a-b+4）2=0，则第三边c的取值范围4＜c＜6．分析 首先根据非负数的性质计算出a、b的值，再根据三角形两边之和大于第三边，三角形的两边差小于第三边可得c的取值范围．
解答 解：由题意得：$\left\{\begin{array}{l}{a+b-6=0}\\{a-b+4=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=1}\\{b=5}\end{array}\right.$，
根据三角形的三边关系定理可得5-1＜c＜5+1，
即4＜c＜6．
故答案为：4＜c＜6．
点评 此题主要考查了非负数的性质，以及三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
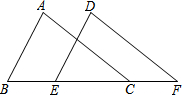已知：如图AB∥DE，AB=DE，BE=CF，此时AC与DF有什么关系？试说明理由．