Question

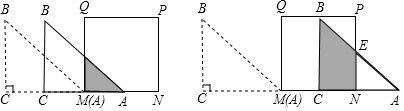
18．如图所示，等腰直角三角形ABC的直角边长于正方形MNPQ的边长均为10cm，边CA与边MN在同一直线上，点A与M重合，让△ABC沿MN方向运动．
（1）当点A与点N重合时停止运动．试写出运动中两个图形重叠部分面积y（cm²）与MA长度x（cm）之间的函数表达式，并指出自变量x的取值范围．
（2）当点C与点M重合后，△ABC继续沿MN方向运动，点C与点N重合时停止运动，试写出运动中两个图形重叠部分面积y（cm²）与MA长度x（cm）之间的函数表达式，并指出自变量x的取值范围．

Answer 1

分析 （1）根据等腰直角三角形的性质和三角形的面积公式计算即可；
（2）根据等腰直角三角形的性质和梯形的面积公式计算即可．

解答 解：（1）依题意有y=$\frac{1}{2}$x²（0≤x≤10）．
（2）依题意有y=$\frac{1}{2}$（x-10+10）（20-x）=$\frac{1}{2}$x²+10x（10≤x≤20）．

点评 本题考查的是正方形和等腰直角三角形的性质，掌握等腰直角三角形的两锐角是45°是解题的关键．