题目内容
8.如图1,某超市从一楼到二楼的电梯AB的长为18米,电梯每级的水平级宽是0.3米.竖直级高是$\frac{\sqrt{3}}{10}$米.(1)求该电梯的坡角∠BAC的度数.
(2)若电梯以每秒上升2级的速度运行,求小明跨上电梯从一楼上升到二楼需要的时间.
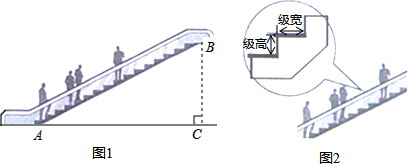
分析 (1)设电梯共有x级,则AC=0.3x米,BC=$\frac{\sqrt{3}}{10}$x米,根据勾股定理求出x的值,进而可得出结论;
(2)设从一楼上升到二楼需要t秒,根据(1)中x的值即可得出结论.
解答 解:(1)∵电梯AB的长为18米,电梯每级的水平级宽是0.3米.竖直级高是$\frac{\sqrt{3}}{10}$米,
∴设电梯共有x级,则AC=0.3x米,BC=$\frac{\sqrt{3}}{10}$x米.
∵AC2+BC2=AB2,即(0.3x)2+($\frac{\sqrt{3}}{10}$x)2=182,解得x=30$\sqrt{3}$,
∴AC=0.3×30$\sqrt{3}$=9$\sqrt{3}$,BC=$\frac{\sqrt{3}}{10}$×30$\sqrt{3}$=9,
∴sin∠BAC=$\frac{9}{18}$=$\frac{1}{2}$,
∴∠BAC=30°;
(2)设从一楼上升到二楼需要t秒,
∵电梯以每秒上升2级的速度运行,x=30$\sqrt{3}$,
∴t=$\frac{30\sqrt{3}}{2}$=15$\sqrt{3}$(秒).
答:从一楼上升到二楼需要的时间是15$\sqrt{3}$秒.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,熟记勾股定理是解答此题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
20.已知等腰△ABC,建立适当的直角坐标系后,其三个顶点的坐标分别为A(m,0).B(m+4,2),C(m+4,-3),则下列关于该三角形三边关系正确的是( )
| A. | AC=BC≠AB | B. | AB=AC≠BC | C. | AB=BC≠AC | D. | AB=AC=BC |
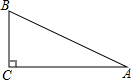 已知:如图,Rt△ABC中,∠C=90°,AC=$\sqrt{10}+\sqrt{2}$,BC=$\sqrt{10}-\sqrt{2}$,求
已知:如图,Rt△ABC中,∠C=90°,AC=$\sqrt{10}+\sqrt{2}$,BC=$\sqrt{10}-\sqrt{2}$,求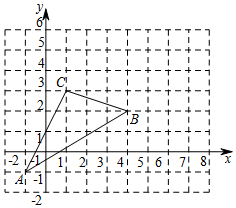 如图,△ABC在直角坐标系中,
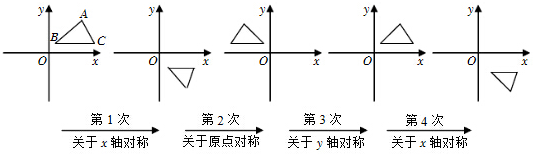
如图,△ABC在直角坐标系中,