题目内容
10.如图(1),两块三角板放置在一起,将△A′B′C绕直角顶点C顺时针旋转一个锐角α成图(2),边A′B′分别交AB,AC于点P,Q,且AQ=PQ,求旋转角α的度数.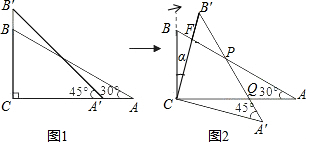
分析 根据等腰三角形的性质得出∠QPA=∠A=30°,利用三角形外角性质得出∠PQC=60°=∠A'+∠QCA'=45°+α,解答即可.
解答 解:∵△APQ为等腰三角形,∠A=30°,
∴∠QPA=∠A=30°,
∴∠PQC=60°=∠A'+∠QCA'=45°+α,
∴α=15°.
点评 此题考查旋转的性质,关键是根据等腰三角形的性质得出∠QPA=∠A=30°,利用三角形外角性质得出∠PQC=60°=∠A'+∠QCA'=45°+α.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
(1)频数分布表中的m=4,n=18;
(2)样本中位数所在成绩的级别是D,扇形统计图中,E组所对应的扇形圆心角的度数是108;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
 某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:成绩频数分布表
| 组别 | 成绩(分) | 频数 |
| A | 50≤x<60 | 6 |
| B | 60≤x<70 | m |
| C | 70≤x<80 | 20 |
| D | 80≤x<90 | 36 |
| E | 90≤x<100 | n |
(2)样本中位数所在成绩的级别是D,扇形统计图中,E组所对应的扇形圆心角的度数是108;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
2.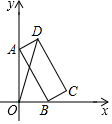 如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )
如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )
 如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )
如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )| A. | 8 | B. | $\sqrt{73}$ | C. | $\sqrt{85}$ | D. | 9 |
20.已知等腰△ABC,建立适当的直角坐标系后,其三个顶点的坐标分别为A(m,0).B(m+4,2),C(m+4,-3),则下列关于该三角形三边关系正确的是( )
| A. | AC=BC≠AB | B. | AB=AC≠BC | C. | AB=BC≠AC | D. | AB=AC=BC |
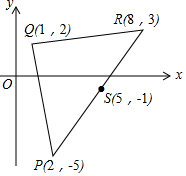 图中的P(2,-5),Q(1,2)和R(8,3)是一个三角形的顶点
图中的P(2,-5),Q(1,2)和R(8,3)是一个三角形的顶点
 已知△ABC的三边长分别为AB=2$\sqrt{5}$,AC=2,BC=4$\sqrt{\frac{1}{2}}$.
已知△ABC的三边长分别为AB=2$\sqrt{5}$,AC=2,BC=4$\sqrt{\frac{1}{2}}$.