题目内容
2.(1)($\frac{1}{10}$)5×$(\frac{1}{10})^{7}$(2)(x2)3;
(3)22003×($\frac{1}{2}$)2004
(4)a3•a3•a2+(a4)2+(-2a2)4
(5)[(a5)3•(b3)2]2
(6)(a2m•an+1)2•am.
分析 (1)根据同底数幂的乘法法则计算即可求解;
(2)根据幂的乘方计算即可求解;
(3)逆用积的乘方计算即可求解;
(4)先算同底数幂的乘法,幂的乘方和积的乘方,再合并同类项即可求解;
(5)先算幂的乘方,再算积的乘方;
(6)先算积的乘方,再根据同底数幂的乘法法则计算即可求解.
解答 解:(1)($\frac{1}{10}$)5×$(\frac{1}{10})^{7}$=($\frac{1}{10}$)12;
(2)(x2)3=x6;
(3)22003×($\frac{1}{2}$)2004
=(2×$\frac{1}{2}$)2003×$\frac{1}{2}$
=1×$\frac{1}{2}$
=$\frac{1}{2}$;
(4)a3•a3•a2+(a4)2+(-2a2)4
=a8+a8+a8
=3a8;
(5)[(a5)3•(b3)2]2
=[a15•b6]2
=a30b12;
(6)(a2m•an+1)2•am.
=a4m•a2n+2•am
=a5m+2n+2.
点评 考查了整式的混合运算,注意:(1)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.(2)“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.同时考查了实数的运算.

练习册系列答案
相关题目
17. 若关于x的不等式x-m>-1的解集如图所示,则m等于( )
若关于x的不等式x-m>-1的解集如图所示,则m等于( )
 若关于x的不等式x-m>-1的解集如图所示,则m等于( )
若关于x的不等式x-m>-1的解集如图所示,则m等于( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$.
一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$.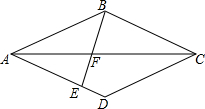 如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.
如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.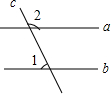 如图,直线a∥b,直线c与a,b相交,∠1=55°,则∠2=125°.
如图,直线a∥b,直线c与a,b相交,∠1=55°,则∠2=125°.
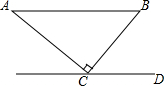 如图,AB∥CE,AC⊥BC,垂足为C,若∠A=35°,则∠BCD=55度.
如图,AB∥CE,AC⊥BC,垂足为C,若∠A=35°,则∠BCD=55度.