题目内容
5．
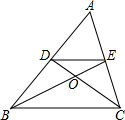如图，△ABC中，BE、CD是AC、AB边上的中线，且BE、CD交于点O，则S△ODE：S四边形DBCE=（ ）| A． | 1：3 | B． | 1：9 | C． | 2：3 | D． | 1：4 |
分析 过点O作OP⊥BC于P，延长PO 交CD于Q，由三角形的中位线定理得到DE∥BC，DE=$\frac{1}{2}BC$，根据相似三角形性质得到OQ=$\frac{1}{2}OP$，利用面积公式即可求解．
解答 
解：过点O作OP⊥BC于P，延长PO 交CD于Q，
∵BE、CD是AC、AB边上的中线，
∴AD=BD，AE=CE，
∴DE∥BC，DE=$\frac{1}{2}BC$，
∴△DEO∽△COB，
∴$\frac{OQ}{OP}$=$\frac{DE}{BC}$=$\frac{1}{2}$，
∴OQ=$\frac{1}{2}OP$，
∴$\frac{{S}_{△ODE}}{{S}_{四边形DBCE}}$=$\frac{\frac{1}{2}DE•OQ}{\frac{1}{2}（DE+BC）•PQ}$=$\frac{DE•OQ}{3DE•3OQ}$=$\frac{1}{9}$．
故选B．
点评 本题考查了三角形的中位线的性质，相似三角形的判定和性质，找准的识别图形是解题的关键．
练习册系列答案
相关题目
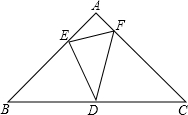△ABC是等腰直角三角形，∠A=90°，AB=$\sqrt{2}$，点D位于边BC的中点上．点E在AB上，点F在AC上，∠EDF=45°，给出以下结论：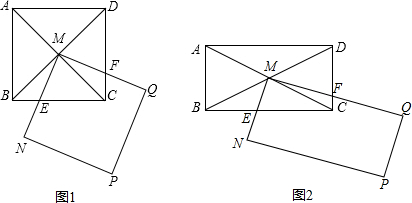
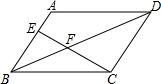如图，在?ABCD中，E是AB边上的一点，连接CE交对角线BD于F，若AE：BE=2：3，则△BEF和△DCF的周长之比为3：5．