题目内容
14．给出一组式子：32+42≡52、82+62≡102、152+82≡172、242+102≡262，根据你发现的规律，写出第五个式子．分析 观察等式的规律，可分别观察等式的左边：第一个的底数分别为：3=22-1，8=32-1，15=42-1，24=52-1，第n个式子为（n+1）2-1，第二个的底数是4，6，8…连续的偶数．右边的底数是比左边的第一个数大2，根据规律即可写出下一个式子规律为：[（n+1）2-1]2+[2（n+1）]2=[（n+1）2+1]2．
解答 解：根据规律，下一个式子是：352+122=372．
点评 此题考查数字的规律问题，关键是根据等式找规律的时候，注意分别观察等式的左边和右边以及左右两边的关系，这需要平时的努力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．
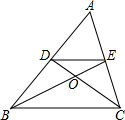如图，△ABC中，BE、CD是AC、AB边上的中线，且BE、CD交于点O，则S△ODE：S四边形DBCE=（ ）
如图，△ABC中，BE、CD是AC、AB边上的中线，且BE、CD交于点O，则S△ODE：S四边形DBCE=（ ）| A． | 1：3 | B． | 1：9 | C． | 2：3 | D． | 1：4 |
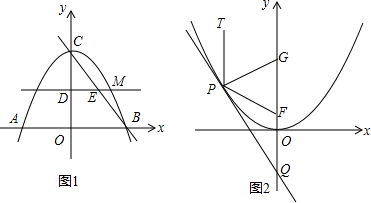
如图，在平面直角坐标系中放置一顶点为A，B，O的直角三角形，将此三角形绕原点O顺时针旋转90°得到△A1B1O．抛物线y=-x2+x+2经过A，B，B1三点．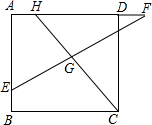
对于一个四边形给出如下定义：有一组对角相等且有一组邻边相等，则称这个四边形为奇特四边形．
在平面直角坐标系中，如果点P的横坐标和纵坐标相等，则称点P为和谐点．例如点（1，1），（-$\frac{1}{3}$，-$\frac{1}{3}$），（-$\sqrt{2}$，-$\sqrt{2}$），…，都是和谐点．