题目内容
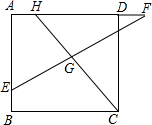
10.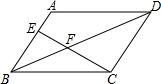 如图,在?ABCD中,E是AB边上的一点,连接CE交对角线BD于F,若AE:BE=2:3,则△BEF和△DCF的周长之比为3:5.
如图,在?ABCD中,E是AB边上的一点,连接CE交对角线BD于F,若AE:BE=2:3,则△BEF和△DCF的周长之比为3:5.
分析 由∠EBF=∠CDF及∠EFB=∠CFD可得两个三角形相似,根据相似三角形的周长比等于对应边的比即可求出.
解答 证明:在平行四边形ABCD中,则AB∥DC,
∴∠EBF=∠CDF,又∠EFB=∠CFD,
∴△BEF∽△DCF.
∵AE:EB=2:3,即BE:CD=3:5,
∴△BEF的周长:△DCF的周长=DC:BE=3:5,
故答案为:3:5.
点评 本题主要考查了平行四边形的性质及相似三角形的判定及性质问题,熟练掌握这些定理是解题的关键.

练习册系列答案
相关题目
1.If we let<a>be the greatest prime number not more than a then the result of the expression<<3>×<25>×<30>>is( )
如果定义<a>为不大于a的最大质数,则<<3>×<25>×<30>>的值为( )
如果定义<a>为不大于a的最大质数,则<<3>×<25>×<30>>的值为( )
| A. | 1333 | B. | 1999 | C. | 2001 | D. | 2249 |
5.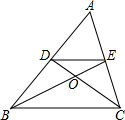 如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )
如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )
 如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )
如图,△ABC中,BE、CD是AC、AB边上的中线,且BE、CD交于点O,则S△ODE:S四边形DBCE=( )| A. | 1:3 | B. | 1:9 | C. | 2:3 | D. | 1:4 |
20.用一副三角板的内角可以画出大于0°且小于180°的不同角度的角共有( )
| A. | 9种 | B. | 10种 | C. | 11种 | D. | 12种 |
 如图,在△ABC中,O是∠ABC与∠ACB的平分线的交点,求证:点O在∠A的平分线上.
如图,在△ABC中,O是∠ABC与∠ACB的平分线的交点,求证:点O在∠A的平分线上.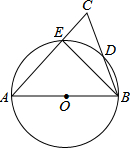 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2.其中正确结论的序号是②④.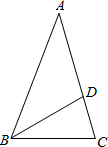 如图,已知△ABC中,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是-1+$\sqrt{5}$.(结果保留根号)
如图,已知△ABC中,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是-1+$\sqrt{5}$.(结果保留根号)
 对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.