题目内容
10.将一个n边形裁剪成一个三角形和一个内角和2520°的多边形,则n=15或16或17.分析 在一个凸n边形的纸板上切下一个三角形,则所得新的多边形的边可能增加一个,也可能不变,也可能减少一个,根据多边形的内角和定理即可求解.
解答 解:设一个内角和为2520°的多边形的边数为x,则
(x-2)×180°=2520°,
解得:x=16.
在一个凸n边形的纸板上切下一个三角形,分三种情况:
①若新多边形的边增加一个,则n的值为15;
②若新多边形的边不变,则n的值为16;
③若新多边形的边减少一个,则n的值为17,
综上所述:n的值为:15或16或17.
故答案为:15或16或17.
点评 本题主要考查了多边形的内角和的计算公式,考查比较新颖,应用了分类思想.理解在一个凸n边形的纸板上切下一个三角形,则所得新的多边形的边可能增加一个,也可能不变,也可能减少一个.是解决本题的关键.

练习册系列答案
相关题目
5.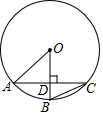 如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
 如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}-1$ |
 我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:
我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图: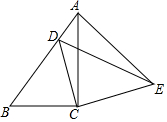 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$.
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$. 如图,正方形ABCD中,点M沿A-D-C运动到C,AN⊥BM,点P为AN的中点,AB=4,则点P的运动的路径长为4.
如图,正方形ABCD中,点M沿A-D-C运动到C,AN⊥BM,点P为AN的中点,AB=4,则点P的运动的路径长为4.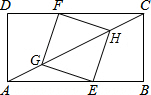 如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.