题目内容
5.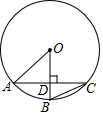 如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )
如图,AC为⊙O的弦,半径OB⊥AC于点D,若∠ACB=22.5°,AD=1,则DB的长度为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}-1$ |
分析 根据圆周角定理可得∠AOB=45°,然后证明AD=DO,进而可利用勾股定理计算出AO长,从而可得BO长,然后利用BO-DO可得BD长度.
解答 解:∵∠ACB=22.5°,
∴∠AOB=45°,
∵OB⊥AC,
∴∠OAD=45°,
∴AD=DO=1,
∴AO=BO=$\sqrt{A{D}^{2}+D{O}^{2}}$=$\sqrt{2}$,
∴DB=$\sqrt{2}$-1,
故选:D.
点评 此题主要考查了勾股定理,以及圆周角定理,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,掌握同圆中,圆心角等于圆周角的2倍.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
13.在平面直角坐标系中,以原点为圆心,1为半径的圆,与直线y=x-$\sqrt{2}$的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
 如图,在五边形ABCDE中,AB∥ED,设∠α=∠A+∠E,∠β=∠B+∠C+∠D,求证:∠β=2∠α.
如图,在五边形ABCDE中,AB∥ED,设∠α=∠A+∠E,∠β=∠B+∠C+∠D,求证:∠β=2∠α.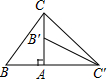 如图,在直角三角形ABC中,∠BAC=90°,∠B=60°,AC=3,将三角形ABC绕点A按顺时针方向旋转90°,得到直角三角形AB'C'(点B'与点B是对应点,点C'与点C是对应点),连接CC',则AC'=3,∠AC'B'=30°,∠AC'C=45°.
如图,在直角三角形ABC中,∠BAC=90°,∠B=60°,AC=3,将三角形ABC绕点A按顺时针方向旋转90°,得到直角三角形AB'C'(点B'与点B是对应点,点C'与点C是对应点),连接CC',则AC'=3,∠AC'B'=30°,∠AC'C=45°.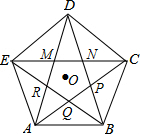 如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR,若AB=$\frac{\sqrt{5}-1}{2}$,则MN=$\sqrt{5}$-2.
如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR,若AB=$\frac{\sqrt{5}-1}{2}$,则MN=$\sqrt{5}$-2.