题目内容
1.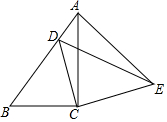 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$.
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$.
分析 根据勾股定理求出AB,根据旋转的性质得出BC=CD=3,DE=AB=5,AC=CE=4,∠BAC=∠DEC,∠BCA=∠DCE=90°,根据相似三角形的判定得出△BCD∽△ACE,求出AE=$\frac{4}{3}$BD,根据勾股定理求出BD,即可求出答案.
解答 解:由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,
∴BC=CD=3,DE=AB=5,AC=CE=4,∠BAC=∠DEC,∠BCA=∠DCE=90°,
∴∠BCD=∠ACE,$\frac{AC}{BC}$=$\frac{CE}{CD}$=$\frac{4}{3}$,
∴△BCD∽△ACE,
∴$\frac{AE}{BD}$=$\frac{4}{3}$,
设BD=x,则AE=$\frac{4}{3}$x,
∵∠BAC=∠DEC,
∴A、D、C、E四点共圆,
∴∠BAE=180°-∠DCE=90°,
在Rt△DAE中,由勾股定理得:AD2+AE2=DE2,
(5-x)2+($\frac{4}{3}$x)2=52,
解得:x=$\frac{9}{5}$,
AE=$\frac{4}{3}$x=$\frac{12}{5}$,
故答案为:$\frac{12}{5}$.
点评 本题考查了勾股定理,旋转的性质,相似三角形的性质和判定等知识点,能求出AE=$\frac{4}{3}$BD是解此题的关键.

练习册系列答案
相关题目
12.观察下表,填表后再解答问题:
(1)试完成下列表格:
(2)第n个图形中有多少个“●”和多少个“★”?
(3)试求第几个图形中有120个“●”?并求该图形中有多少个“★”.
(1)试完成下列表格:
| 序号 | 1 | 2 | 3 | … |
| 图形 |  |  |  | … |
| ●的个数 | 8 | 16 | 24 | … |
| ★的个数 | 1 | 4 | 9 | … |
(3)试求第几个图形中有120个“●”?并求该图形中有多少个“★”.
13.在平面直角坐标系中,以原点为圆心,1为半径的圆,与直线y=x-$\sqrt{2}$的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
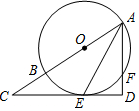 如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C. 如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.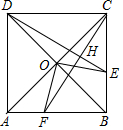 如图,正方形ABCD的对角线AC,BD相交于点O,点E在BC边上,连接DE,作CF⊥DE于点H,H交边AB于点F,连接OE,OF.
如图,正方形ABCD的对角线AC,BD相交于点O,点E在BC边上,连接DE,作CF⊥DE于点H,H交边AB于点F,连接OE,OF.