题目内容
2.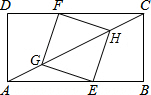 如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.
分析 先根据正方形的性质和矩形的性质,判定△CFO≌△AOE,并求得AO的长,再判定△AOE∽△ABC,求得OECH的长.
解答 解:连接EF交AC于O,
∵四边形EGFH是正方形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,
$\left\{\begin{array}{l}{∠FCO=∠OAB}\\{∠FOC=∠AOE}\\{OF=OE}\end{array}\right.$,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$,
∴CO=AO=$\sqrt{5}$,
∵∠CAB=∠EAO,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴$\frac{OE}{BC}$=$\frac{AO}{AB}$,即 $\frac{OE}{2}$=$\frac{\sqrt{5}}{4}$,
∴OE=$\frac{\sqrt{5}}{2}$=OH,
∴CH=CO-HO=$\sqrt{5}$-$\frac{\sqrt{5}}{2}$=$\frac{\sqrt{5}}{2}$.
故答案为$\frac{\sqrt{5}}{2}$.
点评 本题主要考查了正方形的性质,解决问题的关键是掌握全等三角形的判定与性质,以及相似三角形的判定与性质.本题若不运用相似三角形,则可以过点F作AB的垂线,构造直角三角形,并运用勾股定理进行计算求解.

练习册系列答案
相关题目
12.观察下表,填表后再解答问题:
(1)试完成下列表格:
(2)第n个图形中有多少个“●”和多少个“★”?
(3)试求第几个图形中有120个“●”?并求该图形中有多少个“★”.
(1)试完成下列表格:
| 序号 | 1 | 2 | 3 | … |
| 图形 |  |  |  | … |
| ●的个数 | 8 | 16 | 24 | … |
| ★的个数 | 1 | 4 | 9 | … |
(3)试求第几个图形中有120个“●”?并求该图形中有多少个“★”.
13.在平面直角坐标系中,以原点为圆心,1为半径的圆,与直线y=x-$\sqrt{2}$的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则cos∠ABC的值是$\frac{\sqrt{195}}{25}$.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则cos∠ABC的值是$\frac{\sqrt{195}}{25}$.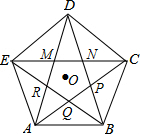 如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR,若AB=$\frac{\sqrt{5}-1}{2}$,则MN=$\sqrt{5}$-2.
如图,连接正五边形ABCDE的各条对角线围成一个新的五边形MNPQR,若AB=$\frac{\sqrt{5}-1}{2}$,则MN=$\sqrt{5}$-2.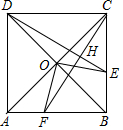 如图,正方形ABCD的对角线AC,BD相交于点O,点E在BC边上,连接DE,作CF⊥DE于点H,H交边AB于点F,连接OE,OF.
如图,正方形ABCD的对角线AC,BD相交于点O,点E在BC边上,连接DE,作CF⊥DE于点H,H交边AB于点F,连接OE,OF.