题目内容
2.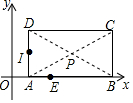 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为(1,0),对角线的交点P的坐标为($\frac{5}{2}$,1).
如图,在直角坐标系中,矩形ABCD的顶点A的坐标为(1,0),对角线的交点P的坐标为($\frac{5}{2}$,1).(1)分别写出顶点B,C,D的坐标.
(2)若在AB上有一点E($\frac{3}{2}$,0),经过点E的直线l能否将矩形ABCD分为面积相等的两部分?若能,求直线l的函数表达式;若不能,请说明理由.
分析 (1)由矩形的性质结合顶点A (1,0),对角线的交点P($\frac{5}{2}$,1),利用中点坐标公式即可求出C点坐标,同理求出C和D点坐标;
(2)设直线解析式为y=kx+b(k≠0),若过E点的直线将矩形ABCD的面积分为相等的两部分,则直线必定过P点,求出k和b的值即可;
解答 解:(1)∵四边形ABCD是矩形,顶点A (1,0),对角线的交点P($\frac{5}{2}$,1),
∴$\frac{1+{x}_{C}}{2}=\frac{5}{2}$,yD=2,
∴C点坐标为(4,2),B点坐标为(4,0),D点坐标为(1,2);
(2)设直线解析式为y=kx+b(k≠0),
∵过E点的直线将矩形ABCD的面积分为相等的两部分,
∴该直线经过点P($\frac{5}{2}$,1),
由题意得$\left\{\begin{array}{l}{\frac{5}{2}k+b=1}\\{\frac{3}{2}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-\frac{3}{2}}\end{array}\right.$.
∴直线解析式为y=x-$\frac{3}{2}$.
点评 本题主要考查一次函数的综合题的知识,解答本题的关键是熟练掌握函数解析式的求法.

练习册系列答案
相关题目
10.为了了解某市八年级5000名学生的平均身高,如果按10%的比例进行抽样调查,在这个问题中,下列说法:①这5000名学生是总体;②每个学生是个体;③500名学生的身高是总体的一个样本;④样本容量是10%,其中说法正确的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
12. 如图,a∥b,∠1是∠2的3倍,则∠2等于( )
如图,a∥b,∠1是∠2的3倍,则∠2等于( )
 如图,a∥b,∠1是∠2的3倍,则∠2等于( )
如图,a∥b,∠1是∠2的3倍,则∠2等于( )| A. | 45° | B. | 90° | C. | 135° | D. | 150° |
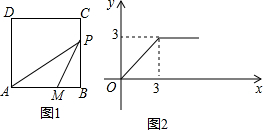 如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示.
如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示. 如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的对补点.
如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的对补点.