题目内容
10.为了了解某市八年级5000名学生的平均身高,如果按10%的比例进行抽样调查,在这个问题中,下列说法:①这5000名学生是总体;②每个学生是个体;③500名学生的身高是总体的一个样本;④样本容量是10%,其中说法正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解答 解:①这5000名学生的平均身高是总体,故①不符合题意;
②每个学生的身高是个体,故②不符合题意;
③500名学生的身高是总体的一个样本,故③符合题意;
④样本容量是500,故④不符合题意;
故选:D.
点评 考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.问题提出:
如图,用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为y,它各边上格点个数之和为x,它内部格点数为n,那么y与x,n有什么数量关系?
问题探究:为解决上述问题,我们采取一般问题特殊化的策略,从最简单的情形入手:
探究一:当格点多边形内部的格点数n=0时,格点多边形的面积y与各边上的格点个数之和x之间的数量关系.
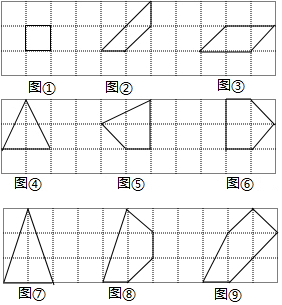
如图①,图②,图③都是n=0时的格点多边形,y与x,n的数量如下表:
分析 表格中数据,可知当n=0时,y与x之间的关系式为y=$\frac{1}{2}$x-1.
探究二:当格点多边形内部的格点数n=1时,格点多边形的面积y与各边上的格点个数之和x之间的数量关系.
如图④,图⑤,图⑥都是n=1时的格点多边形,请完成下表:
分析表格中数据,可知当n=1时,y与x之间的关系式为y=$\frac{1}{2}$x.
探究三:如图⑦,图⑧,图⑨都是n=2时的格点多边形,类比上述探究方法,可知n=2时,y与x之间的关系式为y=$\frac{1}{2}$x+1.
问题解决:
综上可得:格点多边形的面积y,与它各边上格点个数之和x,内部格点数n之间的关系式为y=$\frac{1}{2}$x+n-1.
结论应用:
请用上面的结论计算下面图中格点多边形的面积.(写出计算过程)

如图,用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为y,它各边上格点个数之和为x,它内部格点数为n,那么y与x,n有什么数量关系?
问题探究:为解决上述问题,我们采取一般问题特殊化的策略,从最简单的情形入手:
探究一:当格点多边形内部的格点数n=0时,格点多边形的面积y与各边上的格点个数之和x之间的数量关系.
如图①,图②,图③都是n=0时的格点多边形,y与x,n的数量如下表:
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ① | 0 | 4 | 1 |
| ② | 0 | 5 | 1.5 |
| ③ | 0 | 6 | 2 |
探究二:当格点多边形内部的格点数n=1时,格点多边形的面积y与各边上的格点个数之和x之间的数量关系.
如图④,图⑤,图⑥都是n=1时的格点多边形,请完成下表:
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ④ | 1 | 4 | 2 |
| ⑤ | 1 | 5 | 2.5 |
| ⑥ | 1 |
探究三:如图⑦,图⑧,图⑨都是n=2时的格点多边形,类比上述探究方法,可知n=2时,y与x之间的关系式为y=$\frac{1}{2}$x+1.

问题解决:
综上可得:格点多边形的面积y,与它各边上格点个数之和x,内部格点数n之间的关系式为y=$\frac{1}{2}$x+n-1.
结论应用:
请用上面的结论计算下面图中格点多边形的面积.(写出计算过程)

18.计算($\frac{2}{3}}$)2016×(-$\frac{3}{2}}$)2017的结果是( )
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
15.下列各曲线中表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
19.互为相反数的两个数的和是( )
| A. | 0 | B. | 1 | C. | ±1 | D. | π |
20.下列各式由左边到右边的变形属于因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | 3x2+6x=3x(x+2) | C. | x2-x+1=x(x-1)+1 | D. | a(x-y)=ax-ay |
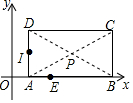 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为(1,0),对角线的交点P的坐标为($\frac{5}{2}$,1).
如图,在直角坐标系中,矩形ABCD的顶点A的坐标为(1,0),对角线的交点P的坐标为($\frac{5}{2}$,1).