题目内容
17.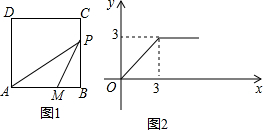 如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示.
如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示.(1)结合图象写出当点P在BC上运动时y与x的函数关系式y=x;(不必写出自变量的取值范围)
(2)求动点P的运动速度及正方形的边长;
(3)补全整个过程中y(cm2)与x(秒)之间的函数图象;
(4)根据(3)中画出的完整图象再赋予一个实际背景.
分析 (1)根据图象容易得出结论;
(2)当点P运动到点C时,△AMP的面积=$\frac{1}{2}$AM•BP=$\frac{1}{2}$×2×ax=3,且动点P的运动时间为3秒,求出a=1即可;得出正方形的边长BC=3cm;
(3)补全图形即可:
(4)根据图象赋予一个实际背景即可.
解答 解:(1)根据图象得:y=x;
故答案为:y=x;
(2)当点P运动到点C时,△AMP的面积=$\frac{1}{2}$AM•BP=$\frac{1}{2}$×2×ax=3,且动点P的运动时间为3秒,
∴$\frac{1}{2}$×2×3a=3,解得:a=1,
即动点P的运动速度为1cm/s;
此时正方形的边长BC=3cm;
(3)如图所示:
(4)答案不唯一,例如:小米的奶奶从家散步到公园,在公园跳广场舞并休息一会儿,然后回家,
其中x轴表示时间,y轴表示小米的奶奶离开家的距离.
点评 本题是四边形综合题目,考查了正方形的性质、三角形面积的计算、函数以及图象等知识;本题综合性强,熟练掌握正方形的性质和图象是解决问题的关键.

练习册系列答案
相关题目
8.若3x=7,3y=$\frac{1}{7}$,则x,y之间的关系为( )
| A. | 互为相反数 | B. | 相等 | C. | 互为倒数 | D. | 无法判断 |
12.某地某一时刻的地面温度为10℃,高度每增加1km,温度下降4℃,则下列说法中:①10℃是常量;②高度是变量;③温度是变量;④该地某一高度这一时刻的温度y(℃)与高度x(km)的关系式为y=10-4x;正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
9.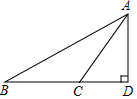 如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )
如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )
 如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )
如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
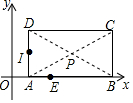 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为(1,0),对角线的交点P的坐标为($\frac{5}{2}$,1).
如图,在直角坐标系中,矩形ABCD的顶点A的坐标为(1,0),对角线的交点P的坐标为($\frac{5}{2}$,1).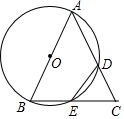 如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.
如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.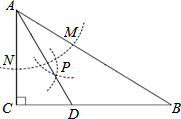 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )