题目内容
13．列方程（组）解应用题：在3月12日植树节活动中，某校七年级（1）班和（2）班共植树52棵，其中七年级（1）班比（2）班多植树8棵，两班各植树多少棵？
分析 设七（1）班植树x棵，七（2）班植树y棵，根据“七年级（1）班和（2）班共植树52棵，其中七年级（1）班比（2）班多植树8棵”列方程组求解可得．
解答 解：设七（1）班植树x棵，七（2）班植树y棵，
根据题意列方程组，得：$\left\{\begin{array}{l}{x+y=52}\\{x-y=5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=30}\\{y=22}\end{array}\right.$，
答：七（1）班植树30棵，七（2）班植树22棵．
点评 本题主要考查二元一次方程组的应用，根据题意确定相等关系，并列出方程是解题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
1．问题提出：
如图，用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形．设格点多边形的面积为y，它各边上格点个数之和为x，它内部格点数为n，那么y与x，n有什么数量关系？
问题探究：为解决上述问题，我们采取一般问题特殊化的策略，从最简单的情形入手：
探究一：当格点多边形内部的格点数n=0时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
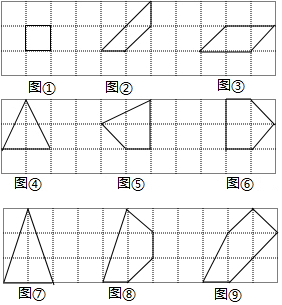
如图①，图②，图③都是n=0时的格点多边形，y与x，n的数量如下表：
分析 表格中数据，可知当n=0时，y与x之间的关系式为y=$\frac{1}{2}$x-1．
探究二：当格点多边形内部的格点数n=1时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
如图④，图⑤，图⑥都是n=1时的格点多边形，请完成下表：
分析表格中数据，可知当n=1时，y与x之间的关系式为y=$\frac{1}{2}$x．
探究三：如图⑦，图⑧，图⑨都是n=2时的格点多边形，类比上述探究方法，可知n=2时，y与x之间的关系式为y=$\frac{1}{2}$x+1．
问题解决：
综上可得：格点多边形的面积y，与它各边上格点个数之和x，内部格点数n之间的关系式为y=$\frac{1}{2}$x+n-1．
结论应用：
请用上面的结论计算下面图中格点多边形的面积．（写出计算过程）
如图，用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形．设格点多边形的面积为y，它各边上格点个数之和为x，它内部格点数为n，那么y与x，n有什么数量关系？
问题探究：为解决上述问题，我们采取一般问题特殊化的策略，从最简单的情形入手：
探究一：当格点多边形内部的格点数n=0时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
如图①，图②，图③都是n=0时的格点多边形，y与x，n的数量如下表：
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ① | 0 | 4 | 1 |
| ② | 0 | 5 | 1.5 |
| ③ | 0 | 6 | 2 |
探究二：当格点多边形内部的格点数n=1时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
如图④，图⑤，图⑥都是n=1时的格点多边形，请完成下表：
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ④ | 1 | 4 | 2 |
| ⑤ | 1 | 5 | 2.5 |
| ⑥ | 1 |
探究三：如图⑦，图⑧，图⑨都是n=2时的格点多边形，类比上述探究方法，可知n=2时，y与x之间的关系式为y=$\frac{1}{2}$x+1．
问题解决：
综上可得：格点多边形的面积y，与它各边上格点个数之和x，内部格点数n之间的关系式为y=$\frac{1}{2}$x+n-1．
结论应用：
请用上面的结论计算下面图中格点多边形的面积．（写出计算过程）
8．若3x=7，3y=$\frac{1}{7}$，则x，y之间的关系为（ ）
| A． | 互为相反数 | B． | 相等 | C． | 互为倒数 | D． | 无法判断 |
18．计算（$\frac{2}{3}}$）2016×（-$\frac{3}{2}}$）2017的结果是（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | $-\frac{3}{2}$ |
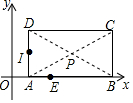如图，在直角坐标系中，矩形ABCD的顶点A的坐标为（1，0），对角线的交点P的坐标为（$\frac{5}{2}$，1）．
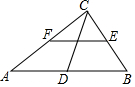如图，在Rt△ABC中，∠ACB=90°，D，E，F分别是AB，BC，AC的中点，若CD=7cm，则EF=7cm．