题目内容
11．某车间原计划用13小时生产一批零件，后来每小时多生产10个，用了12小时，不但完成了任务，而且还多生产零件60个，设原计划每小时生产零件x个，则可列方程为12（x+10）=13x+60．分析 首先理解题意，找出题中存在的等量关系：实际12小时生产的零件数=原计划13小时生产的零件数+60，根据此等式列方程即可．
解答 解：设原计划每小时生产零件x个，则实际每小时生产零件（x+10）个．
根据等量关系列方程得：12（x+10）=13x+60．
故答案为12（x+10）=13x+60．
点评 此题主要考查了由实际问题抽象出一元一次方程，关键是正确理解题意，找出题目中的等量关系，然后再列出方程．
练习册系列答案
相关题目
1．问题提出：
如图，用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形．设格点多边形的面积为y，它各边上格点个数之和为x，它内部格点数为n，那么y与x，n有什么数量关系？
问题探究：为解决上述问题，我们采取一般问题特殊化的策略，从最简单的情形入手：
探究一：当格点多边形内部的格点数n=0时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
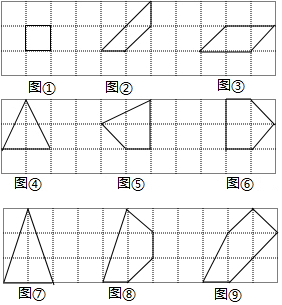
如图①，图②，图③都是n=0时的格点多边形，y与x，n的数量如下表：
分析 表格中数据，可知当n=0时，y与x之间的关系式为y=$\frac{1}{2}$x-1．
探究二：当格点多边形内部的格点数n=1时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
如图④，图⑤，图⑥都是n=1时的格点多边形，请完成下表：
分析表格中数据，可知当n=1时，y与x之间的关系式为y=$\frac{1}{2}$x．
探究三：如图⑦，图⑧，图⑨都是n=2时的格点多边形，类比上述探究方法，可知n=2时，y与x之间的关系式为y=$\frac{1}{2}$x+1．
问题解决：
综上可得：格点多边形的面积y，与它各边上格点个数之和x，内部格点数n之间的关系式为y=$\frac{1}{2}$x+n-1．
结论应用：
请用上面的结论计算下面图中格点多边形的面积．（写出计算过程）
如图，用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形．设格点多边形的面积为y，它各边上格点个数之和为x，它内部格点数为n，那么y与x，n有什么数量关系？
问题探究：为解决上述问题，我们采取一般问题特殊化的策略，从最简单的情形入手：
探究一：当格点多边形内部的格点数n=0时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
如图①，图②，图③都是n=0时的格点多边形，y与x，n的数量如下表：
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ① | 0 | 4 | 1 |
| ② | 0 | 5 | 1.5 |
| ③ | 0 | 6 | 2 |
探究二：当格点多边形内部的格点数n=1时，格点多边形的面积y与各边上的格点个数之和x之间的数量关系．
如图④，图⑤，图⑥都是n=1时的格点多边形，请完成下表：
| 图形序号 | 内部格点数n | 各边上格点个数之和x | 面积y |
| ④ | 1 | 4 | 2 |
| ⑤ | 1 | 5 | 2.5 |
| ⑥ | 1 |
探究三：如图⑦，图⑧，图⑨都是n=2时的格点多边形，类比上述探究方法，可知n=2时，y与x之间的关系式为y=$\frac{1}{2}$x+1．
问题解决：
综上可得：格点多边形的面积y，与它各边上格点个数之和x，内部格点数n之间的关系式为y=$\frac{1}{2}$x+n-1．
结论应用：
请用上面的结论计算下面图中格点多边形的面积．（写出计算过程）
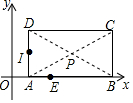如图，在直角坐标系中，矩形ABCD的顶点A的坐标为（1，0），对角线的交点P的坐标为（$\frac{5}{2}$，1）．
19．互为相反数的两个数的和是（ ）
| A． | 0 | B． | 1 | C． | ±1 | D． | π |
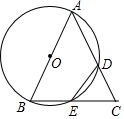如图，在△ABC中，以AB为直径的⊙O分别交AC，BC于点D，E．连接ED，若ED=EC．
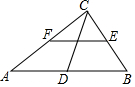如图，在Rt△ABC中，∠ACB=90°，D，E，F分别是AB，BC，AC的中点，若CD=7cm，则EF=7cm．
20．下列各式由左边到右边的变形属于因式分解的是（ ）
| A． | （a+1）（a-1）=a2-1 | B． | 3x2+6x=3x（x+2） | C． | x2-x+1=x（x-1）+1 | D． | a（x-y）=ax-ay |
如图，△ABC是⊙O的内接三角形，∠OBC=55°，则∠A=35°．