题目内容
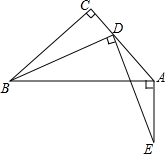 如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE.
如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:在CB上截取作C=CD,由AC=CB得BF=AD,再根据等角的余角相等得到∠ADE=∠DBC,接着判断△CFD和△CAB都是等腰直角三角形,得到∠CFD=∠CDF=∠CBA=∠CAB=45°,所以∠DAE=∠BFD=135°,然后根据“AAS”可判断△BFD≌△ADE,则根据全等的性质即可得到BD=DE.
解答:证明: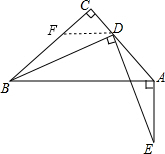 在CB上截取作C=CD,
在CB上截取作C=CD,
∵AC=CB,
∴BF=AD,
∵∠C=90°,BD⊥DE,
∴∠CBD+∠BDC=90°,∠ADE+∠BDC=90°,
∴∠ADE=∠DBC,
∵CF=CD,AC=BC,
∴△CFD和△CAB都是等腰直角三角形,
∴∠CFD=∠CDF=∠CBA=∠CAB=45°,
∴∠DAE=∠BFD=135°,
在△BFD和△ADE中,
,
∴△BFD≌△ADE(AAS),
∴BD=DE.
 在CB上截取作C=CD,
在CB上截取作C=CD,∵AC=CB,
∴BF=AD,
∵∠C=90°,BD⊥DE,
∴∠CBD+∠BDC=90°,∠ADE+∠BDC=90°,
∴∠ADE=∠DBC,
∵CF=CD,AC=BC,
∴△CFD和△CAB都是等腰直角三角形,
∴∠CFD=∠CDF=∠CBA=∠CAB=45°,
∴∠DAE=∠BFD=135°,
在△BFD和△ADE中,
|
∴△BFD≌△ADE(AAS),
∴BD=DE.
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.本题的关键是构造△BFD与△ADE全等.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
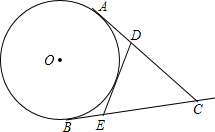 AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.
AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系. 如图,在直角坐标系中,每个小正方形的边长都是单位1.
如图,在直角坐标系中,每个小正方形的边长都是单位1. 如图所示,已知PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.
如图所示,已知PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.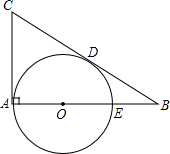 如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )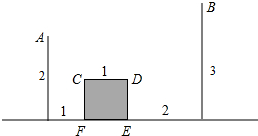 如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于
如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于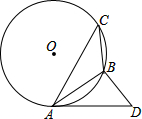 已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B,
已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B,