题目内容
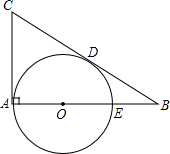 如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,Q是AB上的一点,⊙O分别与AC、BC相切于点A、D,与AB交于另一点E,若BE=2,则切线CD的长为( )A、
| ||
B、2
| ||
C、3
| ||
| D、6 |
考点:切线的性质
专题:计算题
分析:连结OD,如图,根据切线的性质,由BC为⊙O的切线得到OD⊥BC,在Rt△OBD中,根据含30度的直角三角形三边的关系得到OB=2OD,加上OB=OE+BE,所以OD+2=2OD,解得OD=2,再由AC与⊙O相切得到AE=2OD=4,可计算出AB=6,然后在Rt△ABC中根据含30度的直角三角形三边的关系计算出AC,再利用切线长定理得到CD的长.
解答: 解:连结OD,如图,
解:连结OD,如图,
∵BC为⊙O的切线,
∴OD⊥BC,
在Rt△OBD中,∵∠B=30°,
∴OB=2OD,
而OB=OE+BE,
∴OD+2=2OD,解得OD=2,
∵AC与⊙O相切,
∴AE=2OD=4,
∴AB=AE+BE=6,
在Rt△ABC中,∵∠B=30°,
∴AC=
AB=2
,
∴CD=AC=2
.
故选B.
 解:连结OD,如图,
解:连结OD,如图,∵BC为⊙O的切线,
∴OD⊥BC,
在Rt△OBD中,∵∠B=30°,
∴OB=2OD,
而OB=OE+BE,
∴OD+2=2OD,解得OD=2,
∵AC与⊙O相切,
∴AE=2OD=4,
∴AB=AE+BE=6,
在Rt△ABC中,∵∠B=30°,
∴AC=
| ||
| 3 |
| 3 |
∴CD=AC=2
| 3 |
故选B.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
小亮在上午8时、9时、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
| A、上午12时 | B、上午10时 |
| C、上午9时 | D、上午8时 |
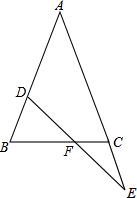 如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.
如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.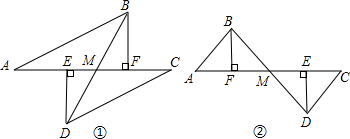
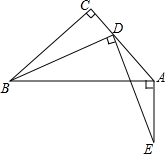 如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE.
如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE.