题目内容
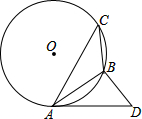 已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B,
已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B,(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,AB=6,求AD的长.
考点:切线的判定
专题:
分析:(1)利用圆周角定理结合切线的判定方法得出∠OAE+∠BAD=90°,即可得出答案;
(2)首先得出△OAE∽△ADB,进而利用相似三角形的性质求出即可.
(2)首先得出△OAE∽△ADB,进而利用相似三角形的性质求出即可.
解答: (1)证明:连接OA,OB,过点O作OE⊥AB于点E,
(1)证明:连接OA,OB,过点O作OE⊥AB于点E,
∵AO=OB,
∴∠OAB=∠OBA,
∵OE⊥AB,
∴∠AOE=∠EOB,
∵∠ACB=∠BAD,
∴∠AOE=∠BAD,
∵∠AOE+∠OAE=90°,
∴∠OAE+∠BAD=90°,
∴AD是⊙O的切线;
(2)解:∵∠AOE=∠BAD,∠AEO=∠ABD=90°,
∴△OAE∽△ADB,
∴
=
,
∵⊙O的半径为5,AB=6,
∴AE=3,则EO=4,
∴
=
,
解得:AD=7.5.
 (1)证明:连接OA,OB,过点O作OE⊥AB于点E,
(1)证明:连接OA,OB,过点O作OE⊥AB于点E,∵AO=OB,
∴∠OAB=∠OBA,
∵OE⊥AB,
∴∠AOE=∠EOB,
∵∠ACB=∠BAD,
∴∠AOE=∠BAD,
∵∠AOE+∠OAE=90°,
∴∠OAE+∠BAD=90°,
∴AD是⊙O的切线;
(2)解:∵∠AOE=∠BAD,∠AEO=∠ABD=90°,
∴△OAE∽△ADB,
∴
| AO |
| AD |
| EO |
| AB |
∵⊙O的半径为5,AB=6,
∴AE=3,则EO=4,
∴
| 5 |
| AD |
| 4 |
| 6 |
解得:AD=7.5.
点评:此题主要考查了相似三角形的判定与性质以及切线的判定等知识,正确掌握相似三角形的判定与性质是解题关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知关于x的方程3x+a-8=0的解是x=2,则a的值是( )
| A、2 | B、3 | C、4 | D、5 |
小亮在上午8时、9时、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
| A、上午12时 | B、上午10时 |
| C、上午9时 | D、上午8时 |
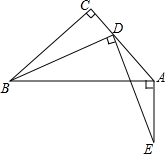 如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE.
如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE. 如图,已知:BE,CF为△ABC的高,P为BE上一点,BP=AC,AQ⊥AP,AQ与CF的延长线交于点Q,求证:AB=QC.
如图,已知:BE,CF为△ABC的高,P为BE上一点,BP=AC,AQ⊥AP,AQ与CF的延长线交于点Q,求证:AB=QC. 如图,抛物线y=y=ax2-8ax+12a与x轴交A、B两点,P在y轴正半轴,PB与抛物线交于C,已知C是BP的中点,∠PBO=45°.
如图,抛物线y=y=ax2-8ax+12a与x轴交A、B两点,P在y轴正半轴,PB与抛物线交于C,已知C是BP的中点,∠PBO=45°. (1)计算:
(1)计算: 如图,已知∠1=∠2,AD=AB,求证:△ABC≌△ADC.
如图,已知∠1=∠2,AD=AB,求证:△ABC≌△ADC.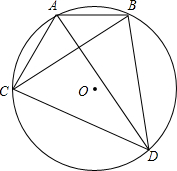 如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为
如图,AD,BC是圆O的两条相互垂直的弦,AB=2,CD=4,则⊙O的半径为