题目内容
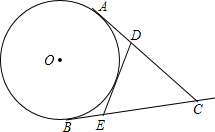 AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.
AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.考点:切线的判定
专题:
分析:如图,作辅助线;证明△AOD≌△OBM,得到OM=OD,此为解题的关键性结论;证明△OME≌△ODE,得到OF=OB,即可解决问题.
解答: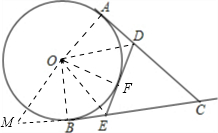 解:DE与⊙O相切;理由如下:
解:DE与⊙O相切;理由如下:
如图,延长CB到M,使BM=AD;连接OA、OB、OE、OD;
过点O作OF⊥DE;
∵AC,BC是⊙O的两条过点C的切线,
∴OA⊥AD,OB⊥BM;
在△AOD与△OBM中,
,
∴△AOD≌△OBM(SAS),
∴OM=OD;
∵AC,BC是⊙O的两条过点C的切线,CA=CB,△CED周长为AC的2倍,
∴DE=AD+BE=MB+BE,即DE=ME;
在△OME与△ODE中,
,
∴△OME≌△ODE(SSS),
∵OB⊥ME,OF⊥DE,
∴OF=OB(全等三角形对应边上的高相等),
∴DE与⊙O相切.
 解:DE与⊙O相切;理由如下:
解:DE与⊙O相切;理由如下:如图,延长CB到M,使BM=AD;连接OA、OB、OE、OD;
过点O作OF⊥DE;
∵AC,BC是⊙O的两条过点C的切线,
∴OA⊥AD,OB⊥BM;
在△AOD与△OBM中,
|
∴△AOD≌△OBM(SAS),
∴OM=OD;
∵AC,BC是⊙O的两条过点C的切线,CA=CB,△CED周长为AC的2倍,
∴DE=AD+BE=MB+BE,即DE=ME;
在△OME与△ODE中,
|
∴△OME≌△ODE(SSS),
∵OB⊥ME,OF⊥DE,
∴OF=OB(全等三角形对应边上的高相等),
∴DE与⊙O相切.
点评:该题主要考查了圆的切线的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用切线的性质定理、判定定理来分析、判断、推理或解答.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
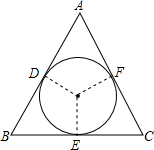 如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.
如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径. 如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为
如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为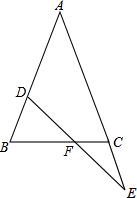 如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE.
如图,△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE. 如图所示,AB=AD,BC=DC,E,F分别是DC、BC的中点,求证:AE=AF.
如图所示,AB=AD,BC=DC,E,F分别是DC、BC的中点,求证:AE=AF.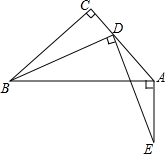 如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE.
如图,在△ABC中,AC=BC,∠C=90°,D是AC边上一点,过A,D分别作AE⊥AB,DE⊥BD,其垂线相交于E,求证:BD=DE. 如图,已知:BE,CF为△ABC的高,P为BE上一点,BP=AC,AQ⊥AP,AQ与CF的延长线交于点Q,求证:AB=QC.
如图,已知:BE,CF为△ABC的高,P为BE上一点,BP=AC,AQ⊥AP,AQ与CF的延长线交于点Q,求证:AB=QC.