题目内容
12．
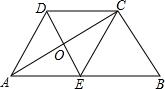如图，在Rt△ABC中，CE是斜边AB上的中线，CD∥AB，且CD=CE，求证：（1）四边形CDEB是平行四边形；
（2）四边形AECD是菱形．
分析 （1）首先根据直角三角形斜边上的中线等于斜边的一半得到AE=CE=BE，从而得到CD=BE，利用一组对边平行且相等证得四边形CDEB是平行四边形；
（2）首先判定四边形AECD是平行四边形，然后根据邻边相等得到四边形AECD是菱形．
解答 证明：（1）∵Rt△ABC中，CE是斜边AB上的中线，
∴AE=CE=BE，
∵CD=CE，
∴CD=BE，
∵CD∥AB，
∴四边形CDEB是平行四边形；
（2）∵CD=AE，
∴四边形AECD是平行四边形，
∵AE=CE，
∴四边形AECD为菱形．
点评 本题考查了平行四边形的判定、菱形的判定，解题的关键是能够熟练掌握菱形及平行四边形的判定定理，难度不大．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
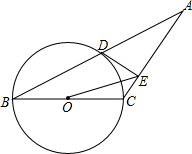如图，在△ABC中，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．
平行四边形ABCD中，EF平行于对角线AC，且与AB，BC分别交于E，F，求证：S△ADE=S△CDF．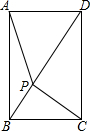
如图，点P是矩形ABCD对角线BD上的一个动点，已知AB=2，BC=$\sqrt{3}$，则PA+PB+PC的最小值是$\sqrt{13}$．