题目内容
2.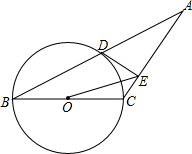 如图,在△ABC中,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
如图,在△ABC中,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.(1)求证:DE是⊙O的切线;
(2)已知:AD=4,AE=3,求⊙O的半径.
分析 (1)首先连接OD,CD,由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD,即可证得OD∥AC,继而可证得结论;
(2)根据三角函数的性质,求得cos∠B=cos∠A=$\frac{AE}{AD}$=$\frac{3}{4}$,继而求得答案.
解答 (1)证明:连接OD,CD,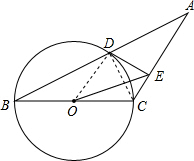
∵BC为⊙O直径,
∴∠BDC=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D点在⊙O上,
∴DE为⊙O的切线;
(2)解:∵DE⊥AC,AD=4,AE=3,
∴cos∠A=$\frac{AE}{AD}$=$\frac{3}{4}$,
由(1)可知∠BDC=90°,BD=AD=4,∠A=∠B,
∴cos∠B=$\frac{BD}{BC}$=$\frac{3}{4}$,
∴$\frac{4}{BC}$=$\frac{3}{4}$,
∴BC=$\frac{16}{3}$,
∴⊙O的半径为$\frac{8}{3}$.
点评 此题考查了切线的判定、三角形中位线的性质、等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
1.光明文具厂工人的工作时间:每月26天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资920元,按月结算.该厂生产A,B两种型号零件,工人每生产一件A种型号零件,可得报酬0.85元,每生产一件B种型号零件,可得报酬1.5元,下表记录的是工人小王的工作情况:
根据上表提供的信息,请回答如下问题:
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目无限制,那么小王该月的工资数目最多为多少?
| 生产A种型号零件/件 | 生产B种型号零件/件 | 总时间/分 |
| 2 | 2 | 70 |
| 6 | 4 | 170 |
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目无限制,那么小王该月的工资数目最多为多少?
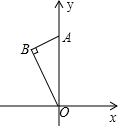 如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( )
如图,含有30°的Rt△AOB的斜边OA在y轴上,且BA=3,∠AOB=30°,将Rt△AOB绕原点O顺时针旋转一定的角度,使直角顶点B落在x轴的正半轴上,得相应的△A′OB′,则A点运动的路程长是( ) 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).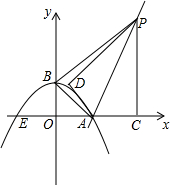 已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.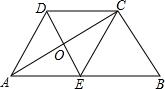 如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证:
如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证: