题目内容
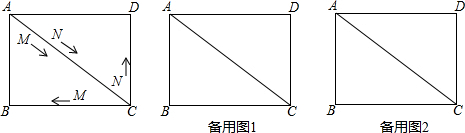
3. 平行四边形ABCD中,EF平行于对角线AC,且与AB,BC分别交于E,F,求证:S△ADE=S△CDF.
平行四边形ABCD中,EF平行于对角线AC,且与AB,BC分别交于E,F,求证:S△ADE=S△CDF.
分析 根据题意连接BD交EF于H,得出S△AED=S△ABD-S△DEH-S△BEH,S△CFD=S△DBC-S△DFH-S△BFH,进而得出答案.
解答 证明: 连接BD交EF于H,
连接BD交EF于H,
则S△ABD=S△DBC,
∵EF∥CA,
∴BD平分EF于H,
∴S△BEH=S△BFH,
S△DEH=S△DFH,
∵S△AED=S△ABD-S△DEH-S△BEH,
S△CFD=S△DBC-S△DFH-S△BFH,
∴S△ADE=S△CDF.
点评 此题主要考查了平行四边形的性质和三角形面积求法,该题主要思路在于所求两个三角形没有公用的底边或高,那么就要想用相等的面积再减去相等的面积,剩余面积相等.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
1.光明文具厂工人的工作时间:每月26天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资920元,按月结算.该厂生产A,B两种型号零件,工人每生产一件A种型号零件,可得报酬0.85元,每生产一件B种型号零件,可得报酬1.5元,下表记录的是工人小王的工作情况:
根据上表提供的信息,请回答如下问题:
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目无限制,那么小王该月的工资数目最多为多少?
| 生产A种型号零件/件 | 生产B种型号零件/件 | 总时间/分 |
| 2 | 2 | 70 |
| 6 | 4 | 170 |
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目无限制,那么小王该月的工资数目最多为多少?
18.已知二次函数y=ax2+bx+c(a≠0)与x轴的交点坐标为A(m,0),B(n,0),点A在点B的左边,当ax2+bx+c=2015时有实数根x1,x2(x1<x2),以下说法中不正确的是( )
| A. | 当a>0时,x1<m<n<x2 | |
| B. | 当a<0时,m<x1<x2<n | |
| C. | 存在m+n=x1+x2 | |
| D. | y=ax2+bx+c-2015与x轴的交点坐标不可能是(x1,0),(x2,0) |
8.下列四个图案中,具有一个共同的性质,则下面选项中的四个数字,满足该性质的是( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
15.小聪在用列表尝试法解二元一次方程组时,因风一吹书翻乱忘记了方程组,可清晰地记得一个方程是x+y=6,不妨设另一个方程为ax+by=m,他尝试列表的部分结果如表:
则a-b=150.
| x | … | 3 | 4 | … |
| y | … | 3 | 2 | … |
| ax+by | … | 1350 | 1500 | … |
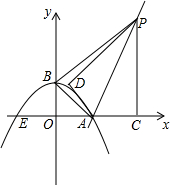 已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.
已知:如图,抛物线y=ax2+bx+c与x轴交于点A(4,0)、E(-2,0)两点,与y轴交于点B(0,2,),连结AB.过点A作直线AK⊥AB,动点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿射线AK运动,设运动时间为t秒,过点P作PC⊥x轴,垂足为C,把△ACP沿AP对折,使点C落在点D处.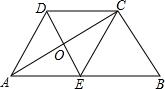 如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证:
如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证: