题目内容
7.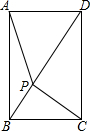 如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.
如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.
分析 将△PBC绕点C逆时针旋转60°,得到△EFC,连接PE,BF,则EF=PB,△PCE是等边三角形,由PE=PC,得出PA+PB+PC=PA+PE+EF,当PA、PE、EF共线时,值最小,然后根据等边三角形的性质和勾股定理求得PA+PB+PC的最小值.
解答  解:将△PBC绕点C逆时针旋转60°,得到△EFC,连接PE,BF,则EF=PB,△PCE是等边三角形,△BFC是等边三角形,
解:将△PBC绕点C逆时针旋转60°,得到△EFC,连接PE,BF,则EF=PB,△PCE是等边三角形,△BFC是等边三角形,
∴PE=PC,
∴PA+PB+PC=PA+PE+EF,当PA、PE、EF共线时,值最小,
连接BF,作FN⊥BC,延长BM=FN,连接MF,则四边形BMFN是矩形,
∴BM=FN,MF=BN,
∵△BCF是等边三角形,
∴FN=$\frac{\sqrt{3}}{2}$BF=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$=$\frac{3}{2}$,BN=$\frac{1}{2}$BF=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$,
∴AM=AB+BM=2+$\frac{3}{2}$=$\frac{7}{2}$,MF=$\frac{\sqrt{3}}{2}$,
∴AC=$\sqrt{A{M}^{2}+M{F}^{2}}$=$\sqrt{13}$,
∴PA+PB+PC的最小值为$\sqrt{13}$,
故答案为$\sqrt{13}$.
点评 本题考查了最短路线问题,矩形的性质,勾股定理的应用,通过旋转得出等边三角形是解题的关键.

练习册系列答案
相关题目
18.已知二次函数y=ax2+bx+c(a≠0)与x轴的交点坐标为A(m,0),B(n,0),点A在点B的左边,当ax2+bx+c=2015时有实数根x1,x2(x1<x2),以下说法中不正确的是( )
| A. | 当a>0时,x1<m<n<x2 | |
| B. | 当a<0时,m<x1<x2<n | |
| C. | 存在m+n=x1+x2 | |
| D. | y=ax2+bx+c-2015与x轴的交点坐标不可能是(x1,0),(x2,0) |
15.小聪在用列表尝试法解二元一次方程组时,因风一吹书翻乱忘记了方程组,可清晰地记得一个方程是x+y=6,不妨设另一个方程为ax+by=m,他尝试列表的部分结果如表:
则a-b=150.
| x | … | 3 | 4 | … |
| y | … | 3 | 2 | … |
| ax+by | … | 1350 | 1500 | … |
19.小明购买文具一共要付32元,小明钱包里只有2元和5元两种面值若干张钱,他一共有几种不同的付款方案( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
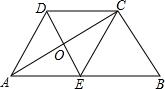 如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证:
如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证: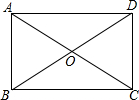 如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.
如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.