题目内容
15.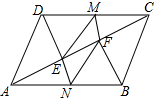 已知:?ABCD中,DE⊥AC于E,BF⊥AC于F,M,N分别是DC,AB的中点.求证:四边形MENF是平行四边形.
已知:?ABCD中,DE⊥AC于E,BF⊥AC于F,M,N分别是DC,AB的中点.求证:四边形MENF是平行四边形.
分析 利用直角三角形斜边中线性质以及平行四边形性质,可以证明EM=FN,EN∥FN,由此可以解决问题.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠DCA=∠CAB,
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEC=∠BFA=90°,
∵DM=MC,AN=NB,
∴EM=MC=DM,NF=NA=NB,
∴∠MCE=∠MEC,∠NAF=∠NFA,
∴∠MEF=∠NFA,
∴EM=FN,EM∥FN,
∴四边形MENF是平行四边形.
点评 本题考查直角三角形斜边中线性质、平行四边形的判定和性质、平行线的判定等知识,熟练掌握这些性质的应用是解决问题的关键,记住平行四边形的五种判定方法,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.
如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.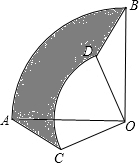 把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.
把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.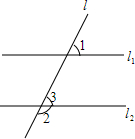 如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).
如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).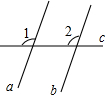 同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行)
同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行)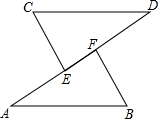 如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.
如图所示,AB∥CD,∠CEA=3∠A,∠BFD=3∠D,试说明:CE∥BF.