题目内容
20.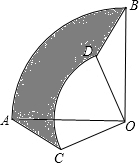 把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.
把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.(1)求证:△AOC≌△BOD;
(2)若OA=3cm,OC=2cm,求阴影部分的面积.
分析 (1)根据90°的角可以证明∠AOC=∠BOD,再根据同一扇形的半径相等,利用边角边定理即可证明三角形全等;
(2)根据扇形面面积公式求出阴影部分的面积.
解答 (1)证明:∵∠COD=∠AOB=90°,
∴∠AOC+∠AOD=∠AOD+∠BOD,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
$\left\{\begin{array}{l}{OC=OD}\\{∠AOC=∠BOD}\\{OA=OB}\end{array}\right.$,
∴△AOC≌△BOD(SAS);
(2)S阴影=S扇形AOB-S扇形COD=$\frac{1}{4}$π×32-$\frac{1}{4}$π×22=$\frac{5}{4}$π(cm2).
答:阴影部分的面积是$\frac{5}{4}π$(cm2).
点评 本题主要考查了全等三角形的判定和如何计算扇形的面积,全等三角形的证明,常用的方法有“边边边”,“边角边”,“角边角”,“角角边”,本题证明得到∠AOC=∠BOD是解题的关键.

练习册系列答案
相关题目
10.已知二次函数y=-x2+(m-1)x+1,当x<1时,y随x的增大而增大,则m的取值范图是( )
| A. | m≥3 | B. | m>3 | C. | m≤-1 | D. | m<-1 |
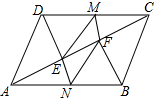 已知:?ABCD中,DE⊥AC于E,BF⊥AC于F,M,N分别是DC,AB的中点.求证:四边形MENF是平行四边形.
已知:?ABCD中,DE⊥AC于E,BF⊥AC于F,M,N分别是DC,AB的中点.求证:四边形MENF是平行四边形. 如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).
如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).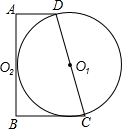 如图所示,直角梯形ABCD中,以腰CD为直径的⊙O1恰与另一腰AB相切,求证:以腰AB为直径的⊙O2也与腰CD相切.
如图所示,直角梯形ABCD中,以腰CD为直径的⊙O1恰与另一腰AB相切,求证:以腰AB为直径的⊙O2也与腰CD相切.