题目内容
7.【探究函数y=x+$\frac{4}{x}$的图象与性质】(1)函数y=x+$\frac{4}{x}$的自变量x的取值范围是x≠0;
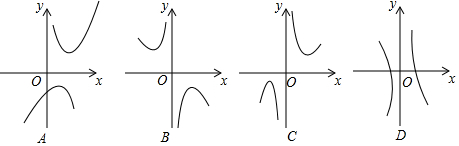
(2)下列四个函数图象中函数y=x+$\frac{4}{x}$的图象大致是C;
(3)对于函数y=x+$\frac{4}{x}$,求当x>0时,y的取值范围.
请将下列的求解过程补充完整.
解:∵x>0
∴y=x+$\frac{4}{x}$=($\sqrt{x}$)2+($\frac{2}{\sqrt{x}}$)2=($\sqrt{x}$-$\frac{2}{\sqrt{x}}$)2+4
∵($\sqrt{x}$-$\frac{2}{\sqrt{x}}$)2≥0
∴y≥4.
[拓展运用]
(4)若函数y=$\frac{{x}^{2}-5x+9}{x}$,则y的取值范围y≥1或y≤-11.
分析 根据反比例函数的性质,一次函数的性质,二次函数的性质解答即可.
解答 解:(1)函数y=x+$\frac{4}{x}$的自变量x的取值范围是x≠0;
(2)函数y=x+$\frac{4}{x}$的图象大致是C;
(3)解:∵x>0
∴y=x+$\frac{4}{x}$=($\sqrt{x}$)2+($\frac{2}{\sqrt{x}}$)2=($\sqrt{x}$-$\frac{2}{\sqrt{x}}$)2+4
∵($\sqrt{x}$-$\frac{2}{\sqrt{x}}$)2≥0
∴y≥4.
(4)①当x>0,y=$\frac{{x}^{2}-5x+9}{x}$=x+$\frac{9}{x}$-5═($\sqrt{x}$)2+($\frac{3}{\sqrt{x}}$)2-5=($\sqrt{x}$-$\frac{3}{\sqrt{x}}$)2+1
∵($\sqrt{x}$-$\frac{3}{\sqrt{x}}$)2≥0,
∴y≥1.
②x<0,y=$\frac{{x}^{2}-5x+9}{x}$=x+$\frac{9}{x}$-5═-[($\sqrt{-x}$)2+($\frac{3}{\sqrt{-x}}$)2+5]=-($\sqrt{-x}$-$\frac{3}{\sqrt{-x}}$)2-11=
∵-($\sqrt{x}$-$\frac{3}{\sqrt{x}}$)2≤0,
∴y≤-11.
故答案为:x≠0,C,4,4,y≥1或y≤-11,
点评 本题考查了反比例函数的性质,一次函数的性质,二次函数的性质,熟记函数的性质是解题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.下列计算结果为x5的是( )
| A. | x3+x2 | B. | x6÷x | C. | (x2)3 | D. | x7-x2 |
17.若1-$\sqrt{3}$是方程x2-2x+c=0的一个根,则c的值为( )
| A. | -2 | B. | 4$\sqrt{3}$-2 | C. | 3-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
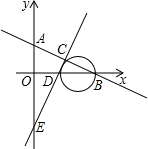 已知直线y=-$\frac{1}{2}$x+1与x轴、y轴分别交于B点、A点,直线y=2x-2与x轴、y轴分别交于D点、E点,两条直线交于点C;
已知直线y=-$\frac{1}{2}$x+1与x轴、y轴分别交于B点、A点,直线y=2x-2与x轴、y轴分别交于D点、E点,两条直线交于点C;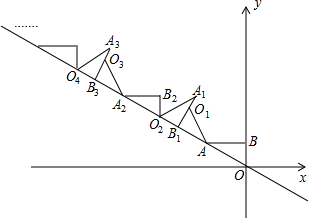 如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.
如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.