题目内容
12．
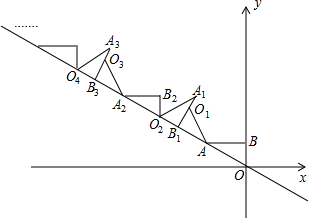如图，AB⊥y轴，垂足为B，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上，再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上，依次进行下去…若点B的坐标是（0，1），则点O12的纵坐标为9+3$\sqrt{3}$．
分析 观察图象可知，O12在直线y=-$\frac{\sqrt{3}}{3}$x时，OO12=6•OO2=6（1+$\sqrt{3}$+2）=18+6$\sqrt{3}$，由此即可解决问题．
解答 解：观察图象可知，O12在直线y=-$\frac{\sqrt{3}}{3}$x时，
OO12=6•OO2=6（1+$\sqrt{3}$+2）=18+6$\sqrt{3}$，
∴O12的横坐标=-（18+6$\sqrt{3}$）•cos30°=-9-9$\sqrt{3}$，
O12的纵坐标=$\frac{1}{2}$OO12=9+3$\sqrt{3}$，
故答案为9+3$\sqrt{3}$．
点评 本题考查坐标与图形的变化、规律型：点的坐标、一次函数的性质等知识，解题的关键是学会从特殊到一般的探究方法，属于中考常考题型．
练习册系列答案
阅读快车系列答案
相关题目
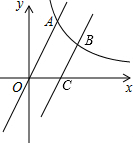如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象与一次函数y=3x的图象相交于点A，其横坐标为2．
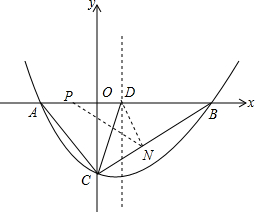已知抛物线y=ax2+bx+c（a＞0）的图象经过点B（14，0）和C（0，-8），对称轴为x=4．
20．某校“阅读写作”社团成员的年龄与人数 情况如图所示：那么该社团成员年龄的中位数是14岁．
| 年龄/岁 | 12 | 13 | 14 | 15 |
| 人数 | 5 | 5 | 15 | 4 |
