题目内容
16.为了解中考体育科目训练情况,某区从九年级学生中抽取了部分学生进行了一次中考体育科测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)求本次抽样测试的学生人数;
(2)求图1中∠α的度数,并把图2条形统计图补充完整;
(3)该区九年级有学生4000名,如果全部参加这次体育测试,请估计不及格的人数大约是多少;
(4)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树状图的方法求出选中小明的概率.
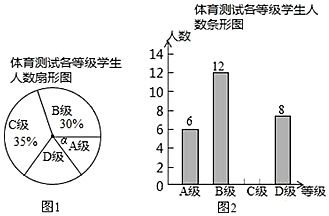
分析 (1)根据B级的人数是12,所占的百分比是30%,据此即可求得总人数;
(2)利用360°乘以对应的百分比即可求得α的值,然后利用百分比的意义求得C级的人数,进而补全直方图;
(3)利用样本估计总体的方法知,全校总人数乘以D级所占的比例,可得答案
(4)利用树状图法列举出所有可能的结果,然后利用概率公式即可求解.
解答 解:(1)12÷30%=40(人);
故答案为:40人;
(2)∠α的度数=360°×$\frac{6}{40}$=54°;
故答案为:54°;
40×35%=14(人);
把条形统计图补充完整,
如图所示:
(3)4000×$\frac{8}{40}$=800(人),
故答案为:800人;
(4)根据题意画树形图如下: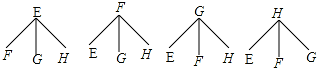
共有12种情况,选中小明的有6种,
则P(选中小明)=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查的是条形统计图和扇形统计图以及用列表法或画树形图法求随机事件的概率的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
11.下列计算正确的是( )
| A. | -(a-b)=-a-b | B. | a2+a2=a4 | C. | a2•a3=a6 | D. | (ab2)2=a2b4 |
8.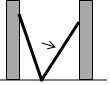 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )| A. | 0.7米 | B. | 1.5米 | C. | 2.2米 | D. | 2.4米 |
6.某市从今年1月1日起调整居民用水价格,每立方米水费上涨$\frac{1}{3}$.小丽家去年12月份的水费是15元,而今年5月的水费则是30元.已知小丽家今年5月的用水量比去年12月的用水量多5m3.求该市今年居民用水的价格.设去年居民用水价格为x元/m3,根据题意列方程,正确的是( )
| A. | $\frac{30}{{({1+\frac{1}{3}})x}}-\frac{15}{x}=5$ | B. | $\frac{30}{{({1-\frac{1}{3}})x}}-\frac{15}{x}=5$ | C. | $\frac{30}{x}-\frac{15}{{({1+\frac{1}{3}})x}}=5$ | D. | $\frac{30}{x}-\frac{15}{{({1-\frac{1}{3}})x}}=5$ |
 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B=56°.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B=56°.