Question

19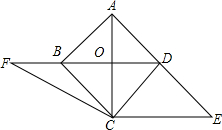．如图，已知正方形ABCD的对角线AC、BD交于点O，CE⊥AC与AD边的延长线交于点E．
（1）求证：四边形BCED是平行四边形；
（2）延长DB至点F，联结CF，若CF=BD，求∠BCF的大小．

Answer 1

分析 （1）利用正方形的性质得出AC⊥DB，BC∥AD，再利用平行线的判定与性质结合平行四边形的判定方法得出答案；
（2）利用正方形的性质结合直角三角形的性质得出∠OFC=30°，即可得出答案．

解答 （1）证明：∵四边形ABCD是正方形，
∴AC⊥DB，BC∥AD，
∵CE⊥AC，
∴∠AOD=∠ACE=90°，
∴BD∥CE，
∴四边形BCED是平行四边形；

（2）解：连接AF，
∵四边形ABCD是正方形，
∴BD⊥AC，BD=AC=2OB=2OC，
即OB=OC，
∴∠OCB=45°，
∵Rt△OCF中，CF=BD=2OC，
∴∠OFC=30°，
∴∠BCF=60°-45°=15°．

点评 此题主要考查了正方形的性质以及平行四边形的判定和直角三角形的性质，正确应用正方形的性质是解题关键．