题目内容
7.先化简,再求值:$\frac{2x-6}{x-2}$÷($\frac{5}{x-2}$-x-2),其中x=-2.分析 先化简括号内的式子,再根据分式的除法进行计算即可化简原式,然后将x=-2代入化简后的式子即可解答本题.
解答 解:$\frac{2x-6}{x-2}$÷($\frac{5}{x-2}$-x-2)
=$\frac{2(x-3)}{x-2}÷\frac{5-(x+2)(x-2)}{x-2}$
=$\frac{2(x-3)}{x-2}×\frac{x-2}{(3+x)(3-x)}$
=-$\frac{2}{x+3}$,
当x=-2时,原式=-$\frac{2}{-2+3}$=-2.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
15.下列事件中,是不确定事件的是( )
| A. | 车辆随机到达一个路口,遇到红灯 | B. | 同位角相等,两条直线平行 | ||
| C. | 平行于同一条直线的两条直线平行 | D. | 对顶角相等 |
2.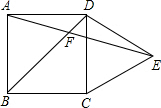 如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
 如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
16.下列命题正确的是( )
| A. | 有且只有一条直线与已知直线垂直 | B. | 同位角相等 | ||
| C. | 两条平行线间的距离处处相等 | D. | 有公共顶点且相等的角是对顶角 |
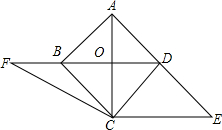 如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E.
如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E.