题目内容
14. 如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )| A. | 25° | B. | 45° | C. | 50° | D. | 70° |
分析 根据角平分线的性质可得∠DBC=∠ABD=25°,然后再计算出∠ACB的度数,再根据线段垂直平分线的性质可得BF=CF,进而可得∠FCB=25°,然后可算出∠ACF的度数.
解答  解:∵BD平分∠ABC,
解:∵BD平分∠ABC,
∴∠DBC=∠ABD=25°,
∵∠A=60°,
∴∠ACB=180°-60°-25°×2=70°,
∵BC的中垂线交BC于点E,
∴BF=CF,
∴∠FCB=25°,
∴∠ACF=70°-25°=45°,
故选:B.
点评 本题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
2.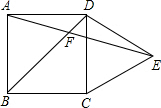 如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
 如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
9.若三角形的三边长分别为$\sqrt{2}$,$\sqrt{6}$,2,则此三角形的面积为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
6. 如图,?ABCD 中. EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
如图,?ABCD 中. EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
 如图,?ABCD 中. EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
如图,?ABCD 中. EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )| A. | 13 | B. | 14 | C. | 15 | D. | 18 |
3. 如图,直线l1∥l2,∠A=125°,∠B=105°,则∠1+∠2=( )°.
如图,直线l1∥l2,∠A=125°,∠B=105°,则∠1+∠2=( )°.
 如图,直线l1∥l2,∠A=125°,∠B=105°,则∠1+∠2=( )°.
如图,直线l1∥l2,∠A=125°,∠B=105°,则∠1+∠2=( )°.| A. | 230 | B. | 20 | C. | 50 | D. | 90 |

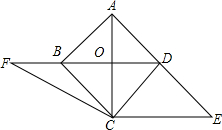 如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E.
如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E. 如图,在梯形ABCD中,AD∥BC,AD=1,BC=4,AC=3,BD=4,则梯形ABCD的面积为6.
如图,在梯形ABCD中,AD∥BC,AD=1,BC=4,AC=3,BD=4,则梯形ABCD的面积为6.