题目内容
1．
如图，在3×3的方格内，填写了一些单项式，已知图中各行、各列及对角线上三个单项式之和都相等，则x的值应为-1．
分析 根据题意得出方程组，求出方程组的解即可．
解答 解：根据题意得：2x+3+2=2-3+4y且2x+y+4y=2x+3+2，
解得：x=-1，y=1，
故答案为：-1．
点评 本题考查了合并同类项和二元一次方程组，能根据题意列出算式是解此题的关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
11．
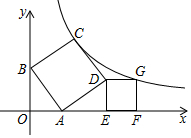如图，正方形ABCD和正方形DEFG放置在直角坐标系中，点A，E，F在x轴的正半轴，点B在y轴的正半轴上，点C，G均在函数y=$\frac{k}{x}$的图象上，若AB=$\sqrt{3}$，则k的值是（ ）
如图，正方形ABCD和正方形DEFG放置在直角坐标系中，点A，E，F在x轴的正半轴，点B在y轴的正半轴上，点C，G均在函数y=$\frac{k}{x}$的图象上，若AB=$\sqrt{3}$，则k的值是（ ）| A． | 2$+\sqrt{2}$ | B． | 3+$\frac{3}{2}\sqrt{2}$ | C． | $\sqrt{2}$ | D． | 3.6 |
在同一条件下，同一型号的30辆汽车进行耗油1L所行驶的路程的试验，将结果绘制如下频数分布直方图，根据统计图解答下列问题：
9．
如图所示，左边的正方形与右边的扇形面积相等，扇形的半径和正方形的边长都是2cm，则此扇形的弧长为（ ）cm．
如图所示，左边的正方形与右边的扇形面积相等，扇形的半径和正方形的边长都是2cm，则此扇形的弧长为（ ）cm．| A． | 4 | B． | 4π | C． | 8 | D． | 8-π |
6．
小李同学在求一元二次方程-2x2+4x+1=0的近似根时，先在直角坐标系中使用软件绘制了二次函数y=-2x2+4x+1的图象（如图），接着观察图象与x轴的交点A和B的位置，然后得出该一元二次方程两个根的范围是-1＜x1＜0，2＜x2＜3，小李同学的这种方法主要运用的数学思想是（ ）
小李同学在求一元二次方程-2x2+4x+1=0的近似根时，先在直角坐标系中使用软件绘制了二次函数y=-2x2+4x+1的图象（如图），接着观察图象与x轴的交点A和B的位置，然后得出该一元二次方程两个根的范围是-1＜x1＜0，2＜x2＜3，小李同学的这种方法主要运用的数学思想是（ ）| A． | 公理化 | B． | 类比思想 | C． | 数形结合 | D． | 模型思想 |
13．
如图，一圆柱体的底面圆周长为20cm，高AB为4cm，BC是上底的直径，一只蚂蚁从点A出发，沿着圆柱的表面爬行到点C，则爬行的最短路程是（ ）
如图，一圆柱体的底面圆周长为20cm，高AB为4cm，BC是上底的直径，一只蚂蚁从点A出发，沿着圆柱的表面爬行到点C，则爬行的最短路程是（ ）| A． | 2$\sqrt{29}$ | B． | $\frac{4}{π}$$\sqrt{{π}^{2}+25}$ | C． | 2$\sqrt{25{π}^{2}+4}$ | D． | 14 |
