题目内容
16．（1）化简：$\frac{1}{x+1}$-$\frac{2}{1-{x}^{2}}$（2）关于x的一元二次方程kx2-2x+3=0有两个不相等的实数根．求：k的取值范围．
分析 （1）先把分母因式分解得到最简共分母，然后通分后进行通分母的加法运算；
（2）根据一元二次方程的定义和判别式的意义得到k≠0且△=（-2）2-4k•3＞0，然后求出两个不等式的公共部分即可．
解答 解：（1）原式=$\frac{1}{x+1}$+$\frac{1}{（x+1）（x-1）}$
=$\frac{x-1+1}{（x+1）（x-1）}$
=$\frac{x}{{x}^{2}-1}$；
（2）根据题意得k≠0且△=（-2）2-4k•3＞0，
解得k＜$\frac{1}{3}$且k≠0．
点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程无实数根．也考查了分式的加减法．
练习册系列答案
相关题目
如图，在菱形ABCD中，BD=8，tan∠ABD=$\frac{3}{4}$，点P从点B出发，沿着菱形的对角线出发运动到点D，过点P作BD的垂线，分别与AB、BC或AD、CD交于点E、F，过点E、F作BD的平行线，构造矩形EFGH，设矩形EFGH的面积为y，点P运动的路程为x，则y与x的函数图象大致是（ ）
7．
如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A、B重合），作CD⊥OB于点D，若点C，D都在双曲线y=$\frac{k}{x}$上（x＜0），则k的值为（ ）
如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A、B重合），作CD⊥OB于点D，若点C，D都在双曲线y=$\frac{k}{x}$上（x＜0），则k的值为（ ）| A． | -9 | B． | -9$\sqrt{3}$ | C． | -18$\sqrt{3}$ | D． | -25$\sqrt{3}$ |
4．为了“天更蓝，水更绿”某市政府加大了对空气污染的治理力度，经过几年的努力，空气质量明显改善，现收集了该市连续30天的空气质量情况作为样本，整理并制作了如下表格和一幅不完整的条形统计图：
说明：环境空气质量指数（AQI）技术规定：ω≤50时，空气质量为优；51≤ω≤100时，空气质量为良；101≤ω≤150时，空气质量为轻度污染；151≤ω≤200时，空气质量为中度污染，…
根据上述信息，解答下列问题：
（1）直接写出空气污染指数这组数据的众数90，中位数90；
（2）请补全空气质量天数条形统计图；
（3）根据已完成的条形统计图，制作相应的扇形统计图；
（4）健康专家温馨提示：空气污染指数在100以下适合做户外运动．请根据以上信息，估计该市居民一年（以365天计）中有多少天适合做户外运动？
| 空气污染指数（ω） | 30 | 40 | 70 | 80 | 90 | 110 | 120 | 140 |
| 天数（t） | 1 | 2 | 3 | 5 | 7 | 6 | 4 | 2 |
根据上述信息，解答下列问题：
（1）直接写出空气污染指数这组数据的众数90，中位数90；
（2）请补全空气质量天数条形统计图；
（3）根据已完成的条形统计图，制作相应的扇形统计图；
（4）健康专家温馨提示：空气污染指数在100以下适合做户外运动．请根据以上信息，估计该市居民一年（以365天计）中有多少天适合做户外运动？
如图，在3×3的方格内，填写了一些单项式，已知图中各行、各列及对角线上三个单项式之和都相等，则x的值应为-1．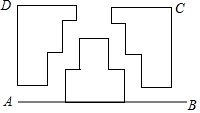
如图，四边形ABCD是一块长方形场地，AB=42米，AD=25米，从A，B两处入口的小路宽都为1米，两小路回合处路宽为2米，其余部分种植草坪，则草坪面积为960平方米．