Question

11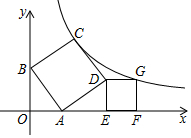．如图，正方形ABCD和正方形DEFG放置在直角坐标系中，点A，E，F在x轴的正半轴，点B在y轴的正半轴上，点C，G均在函数y=$\frac{k}{x}$的图象上，若AB=$\sqrt{3}$，则k的值是（　　）

• A． 2$+\sqrt{2}$
• B． 3+$\frac{3}{2}\sqrt{2}$
• C． $\sqrt{2}$
• D． 3.6

Answer 1

分析 过点C作CH⊥y轴于点H，易证△BAO≌△ADE，△ABO≌△CBH，从而可知HB=OB=AE，HB=OA=DE，设G的坐标为（x，y），从而可求出点C的坐标（x-2y，x-y），利用勾股定理即可求出x与y的值，从而可求出k的值．

解答 解：过点C作CH⊥y轴于点H，
∵正方形ABCD和正方形DEFG，
∴AB=AD，ED=FG=EF，∠BAD=90°
∴∠BAO+∠DAE=∠DAE+∠ADE=90°，
∴∠BAO=∠ADE，
在△BAO与△ADE中，
$\left\{\begin{array}{l}{∠BAO=∠ADE}\\{∠BOA=∠AED}\\{AB=AD}\end{array}\right.$
∴△BAO≌△ADE（AAS）
∴OA=DE，OB=AE，
同理可证：△ABO≌△CBH，
∴CH=OB，HB=OA
设G（x，y），
∴DE=EF=FG=y，OF=x，
∴OA=HB=y，
∴AE=OB=x-2y，
∴OH=OB+HB=x-y，
∴C的坐标为（x-2y，x-y），
∵点C与点G在反比例函数图象上，
∴（x-2y）（x-y）=xy，
∴x²-4xy+2y²=0，
在Rt△AOB中，
由勾股定理可知：（x-2y）²+y²=3，
∴x²-4xy+5y²=3，
∴y²=3，
∴y=1，
∴x²-4x+2=0，
∴x=2±$\sqrt{2}$，
当x=2-$\sqrt{2}$时，
∴x-2y=2-$\sqrt{2}$-2=-$\sqrt{2}$＜0，不符合题意，
当x=2+$\sqrt{2}$，
∴k=xy=2+$\sqrt{2}$，
故选（A）

点评 本题考查反比例函数的综合问题，涉及勾股定理、全等三角形的性质与判定，解方程等知识，属于中等题型．