题目内容
3.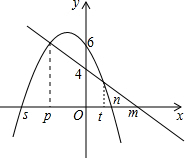 如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).
如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).
分析 由已知条件得出y1=kx+4,y2=ax2+bx+6,当y1=y2时,得出ax2+(b-k)x+2=0,由两个函数图象交点的横坐标分别为p、t,得出方程的解x1=p,x2=t,即可得出结果.
解答 解:∵一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),
∴y1=kx+4,
∵y2=ax2+bx+c,与y轴交于(0,6),
∴y2=ax2+bx+6,
当y1=y2时,ax2+bx+c=kx+4,
∴ax2+(b-k)x+2=0,
∵两个函数图象交点的横坐标分别为p、t,
∴x1=p,x2=t,
∴y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0);
故答案为:(p,0)和(t,0).
点评 本题考查了抛物线与x轴的交点以及与一元二次方程的解的关系;根据题意得出y3=ax2+(b-k)x+2的图象与x轴的交点坐标是解决问题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
11.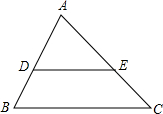 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
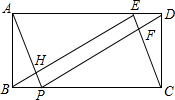 如图,矩形ABCD中,AB=2,BC=5,E、F分别在边AD,BC上,且DE=BP=1.
如图,矩形ABCD中,AB=2,BC=5,E、F分别在边AD,BC上,且DE=BP=1. 如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.
如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.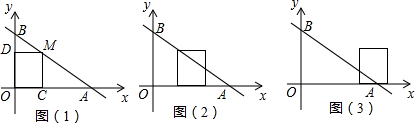
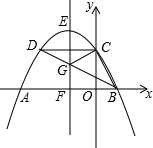 如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.
如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.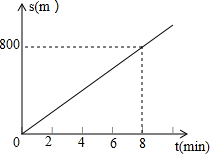 小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题:
小灰灰和灰太狼一起进行晨练,小灰灰从狼堡先跑8分钟后,灰太狼才从同一起点沿同一路线开始跑,它们的速度一直保持不变,经过2分钟后两人相遇,小灰灰跑过的路程s和所用的时间t之间的关系如图所示,根据图象回答下列问题: