题目内容
6.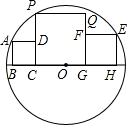 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}+1$ | D. | 2$\sqrt{2}$ |
分析 连接AO、PO、EO,设⊙O的半径为r,OC=x,OG=y,列出方程组即可解决问题.
解答 解:连接AO、PO、EO,设⊙O的半径为r,OC=x,OG=y,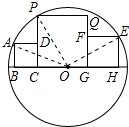
由勾股定理可知:$\left\{\begin{array}{l}{{r}^{2}={1}^{2}+(x+1)^{2}}&{①}\\{{r}^{2}={x}^{2}+(x+y)^{2}}&{②}\\{{r}^{2}=(y+2)^{2}+{2}^{2}}&{③}\end{array}\right.$
②-③得到:x2+(x+y)2-(y+2)2-22=0,
∴(x+y)2-22=(y+2)2-x2,
∴(x+y+2)(x+y-2)=(y+2+x)(y+2-x),
∵x+y+2≠0,
∴x+y-2=y+2-x,
∴x=2,代入①得到r2=10,代入②得到:10=4+(x+y)2,
∴(x+y)2=6,
∵x+y>0,
∴x+y=$\sqrt{6}$,
∴y=$\sqrt{6}$-2.
∴CG=x+y=$\sqrt{6}$.
故选B.
点评 本题考查正方形的性质、圆、勾股定理等知识,解题的关键是设未知数列方程组解决问题,难点是解方程组,利用因式分解法巧妙求出x的值,学会把问题转化为方程组,用方程组的思想去思考问题.

练习册系列答案
相关题目
11.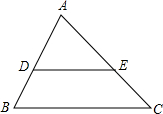 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
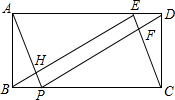 如图,矩形ABCD中,AB=2,BC=5,E、F分别在边AD,BC上,且DE=BP=1.
如图,矩形ABCD中,AB=2,BC=5,E、F分别在边AD,BC上,且DE=BP=1. 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数.
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数. 如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.
如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.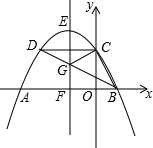 如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.
如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$. 三角形在正方形方格纸中的位置如图所示,则cosα的值是$\frac{4}{5}$.
三角形在正方形方格纸中的位置如图所示,则cosα的值是$\frac{4}{5}$.