题目内容
10.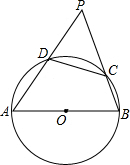 如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P
如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P(1)求证:△CDP∽△ABP;
(2)若AD=PD=3,PC=2$\sqrt{3}$,分别求AB,CD的长.
分析 (1)由四边形ABCD是圆内接四边形,得到∠PCD=∠A,根据相似三角形的判定定理即可得到结论;
(2)连接BD,由AB是半圆O的直径,得到BD⊥AP,于是得到AB=PB,根据相似三角形的性质得到$\frac{PD}{PC}=\frac{PB}{PA}$,求得AB=PB=3$\sqrt{3}$,然后根据相似三角形的性质得到结论.
解答 (1)证明:∵四边形ABCD是圆内接四边形,
∴∠PCD=∠A,
∵∠P=∠P,
∴△CDP∽△ABP;
(2)解:连接BD,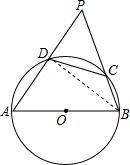 ∵AB是半圆O的直径,
∵AB是半圆O的直径,
∴BD⊥AP,
∵AD=PD,
∴AB=PB,
∵△CDP∽△ABP,
∴$\frac{PD}{PC}=\frac{PB}{PA}$,
∵AD=PD=3,PC=2$\sqrt{3}$,
∴PB=$\frac{3×6}{2\sqrt{3}}$=3$\sqrt{3}$,
∴AB=PB=3$\sqrt{3}$,
∵△CDP∽△ABP,
∴$\frac{CD}{AB}=\frac{PD}{PB}$,
∴CD=$\frac{3\sqrt{3}×3}{3\sqrt{3}}$=3.
点评 本题考查了相似三角形的判定和性质,圆内接四边形的性质,圆周角定理,线段垂直平分线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
1.由10个非负整数构成的一组数据x1,x2,…,x10.当它们的平均数、众数、中位数满足下列选项中的哪个时,可以保证x1,x2,…,x10中最大的数据一定不超过7.( )
| A. | 平均数为2,众数为2,中位数为2 | B. | 平均数为3,众数为2,中位数为4 | ||
| C. | 平均数为2,众数为3,中位数为2 | D. | 平均数为2,众数为3,中位数为4 |
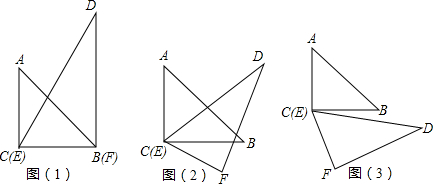
 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数.
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数. 如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.
如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.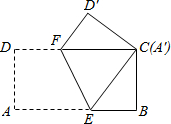 如图,将长为4cm,宽为2cm的矩形纸片ABCD沿着EF翻叠,使点A与C重合,则折痕EF的长为$\sqrt{5}$cm.
如图,将长为4cm,宽为2cm的矩形纸片ABCD沿着EF翻叠,使点A与C重合,则折痕EF的长为$\sqrt{5}$cm.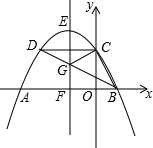 如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.
如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.


