题目内容
2.先观察下列等式,再回答下列问题:①$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{1+1}$=1$\frac{1}{2}$;
②$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=1+$\frac{1}{2}$-$\frac{1}{2+1}$=1$\frac{1}{6}$;
③$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=1+$\frac{1}{3}$-$\frac{1}{3+1}$=1$\frac{1}{12}$.
(1)请你根据上面三个等式提供的信息,猜想$\sqrt{1+\frac{1}{{5}^{2}}+\frac{1}{{6}^{2}}}$的结果,并验证;
(2)请你按照上面各等式反映的规律,试写出用含n的式子表示的等式(n为正整数).
分析 (1)根据观察,可发现规律,根据规律,可得答案;
(2)根据观察,可发现规律$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=1$\frac{1}{n(n+1)}$.
解答 解:(1)$\sqrt{1+\frac{1}{{5}^{2}}+\frac{1}{{6}^{2}}}$=1+$\frac{1}{5}$-$\frac{1}{6}$=1$\frac{1}{30}$,
$\sqrt{1+\frac{1}{{5}^{2}}+\frac{1}{{6}^{2}}}$=$\sqrt{1+\frac{1}{25}+\frac{1}{36}}$=$\sqrt{\frac{25×36+36+25}{25×36}}$=$\sqrt{\frac{3{1}^{2}}{3{0}^{2}}}$=$\frac{31}{30}$=1$\frac{1}{30}$;
(2)$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=1$\frac{1}{n(n+1)}$.
点评 本题考查了二次根式的性质与化简,观察发现规律$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$=1$\frac{1}{n(n+1)}$是解题关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
7.在实数$\root{3}{-1}$、0、$\sqrt{3}$、$\frac{22}{5}$中,无理数是( )
| A. | $\root{3}{-1}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $\frac{22}{5}$ |
 已知函数y=-x2-2x+3.
已知函数y=-x2-2x+3.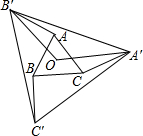 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′. 图中一共有多少个三角形?锐角三角形、直角三角形、钝角三角形各有多少个?用符号表示这些三角形.
图中一共有多少个三角形?锐角三角形、直角三角形、钝角三角形各有多少个?用符号表示这些三角形. 如图,求∠A+∠B+∠OCD+∠ODC+∠E+∠F的度数.
如图,求∠A+∠B+∠OCD+∠ODC+∠E+∠F的度数.