题目内容
13.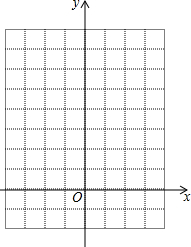 已知函数y=-x2-2x+3.
已知函数y=-x2-2x+3.(1)配方后得y=-(x+1)2+4,开口方向是下、对称轴是直线x=-1 和顶点坐标(-1,4);
(2)分别求出抛物线与x轴和y轴的交点是(-3,0),(1,0),(0,3);
(3)在如图中画出这个函数在x轴上方的图象.
分析 (1)根据配方法把一般式化为顶点式,根据二次函数的性质得到答案.
(2)分别令y=0,x=0,解方程即可求得交点坐标;
(3)根据顶点坐标进而解得坐标画出图象即可.
解答 解:(1)y=-x2-2x+3
=-(x2+2x+1)+4
=-(x+1)2+4,
则抛物线开口向下,对称轴是x=-1,顶点坐标是(-1,4).
(2)令y=0,则,-x2-2x+3=0,
解得x1=-3,x2=1,
∴抛物线与x轴的交点坐标为(-3,0),(1,0),
令x=0,则y=-x2-2x+3=3,
∴抛物线与y轴的交点坐标为(0,3);
(3)画出这个函数在x轴上方的图象如图:
故答案为:-(x+1)2+4,下,x=-1,(-1,4);(-3,0),(1,0),(0,3).
点评 本题考查的是配方法的应用和二次函数的性质,掌握配方法的一般步骤、根据解析式确定开口方向、对称轴和顶点坐标是就的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.据统计,2014年3月(共31天)北京市空气质量等级天数如下表所示:
(1)请根据所给信息补全统计表;
(2)市环保局正式发布了北京PM2.5来源的最新研究成果,专家通过论证已经分析出汽车尾气排放是本地主要污染源.在北京市小客车数量调控方案中,将逐年增加新能源小客车的指标.已知2014年的指标为2万辆,计划2016年的指标为6万辆,假设2014~2016年新能源小客车指标的年增长率相同且均为x,求这个年增长率x.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449)
| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 5 | 11 | 3 | 7 | 2 | 3 |
(2)市环保局正式发布了北京PM2.5来源的最新研究成果,专家通过论证已经分析出汽车尾气排放是本地主要污染源.在北京市小客车数量调控方案中,将逐年增加新能源小客车的指标.已知2014年的指标为2万辆,计划2016年的指标为6万辆,假设2014~2016年新能源小客车指标的年增长率相同且均为x,求这个年增长率x.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449)
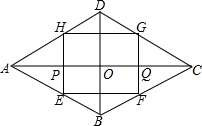 如图,在菱形ABCD中,两条对角线长是AC=10,BD=6,F是线段AO上一点(不与A、O重合),Q是线段OC上一点,且AP=CQ,分别将∠BAD和∠BCD折叠,使A、C两点都在对角线AC上,折痕分别是EH和FG,EH过P点,FG过Q点,连接EF、HG,再把折叠部分铺平.
如图,在菱形ABCD中,两条对角线长是AC=10,BD=6,F是线段AO上一点(不与A、O重合),Q是线段OC上一点,且AP=CQ,分别将∠BAD和∠BCD折叠,使A、C两点都在对角线AC上,折痕分别是EH和FG,EH过P点,FG过Q点,连接EF、HG,再把折叠部分铺平. 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.