题目内容

10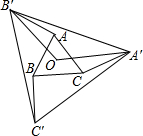．如图，O是边长为1的等边△ABC的中心，将AB、BC、CA分别绕点A、点B、点C顺时针旋转α（0°＜α＜180°），得到AB′、BC′、CA′，连接A′B′、B′C′、A′C′、OA′、OB′．
（1）∠A′OB′=120°；
（2）当α=150°时，△A′B′C′的周长最大．

分析 （1）△A'B'C'是等边三角形，根据中心角的定义求解；
（2）当O，A，B'三点在一条直线上时，B'在OA的延长线上时，OB'最大，A′B′C′边长最大，则△A′B′C′的周长最大．

解答 解：（1）∠A′OB′=$\frac{360°}{3}$=120°，
故答案是：120；
（2）△A'B'C'是等边三角形，△A′B′C′的周长最大，则边长最大，则OB'最大，当O，A，B'三点在一条直线上时，B'在OA的延长线上，OB'最大．
∠BAO=$\frac{1}{2}$∠BAC=30°，
则a=180°-30°=150°．
故答案是：150．

点评 本题考查了三角形的旋转，正确理解△A′B′C′的周长最大的条件是关键．

练习册系列答案
相关题目
20．把下列各数填入相应的括号内：
-1.2，0，1，$\frac{π}{2}$，-1.010010001，…，$\frac{22}{7}$，-0.$\stackrel{•}{0}$$\stackrel{•}{2}$
（1）正数集合：{                                …}；
（2）负数集合：{                                …}；
（3）有理数集合：{                              …}；
（4）无理数集合：{                               …}．
1．化简：
（1）2a-5b-3a+b
（2）4a2-2（7ab-1）+3（3ab-4a2）
18．把抛物线y=ax2+bx+c的图象先向右平移3个单位，再向下平移2个单位，所得的图象解析式是y=x2-2x+5，则a+b+c=15．
5．如图，BE与CD相交于点A，CF为∠BCD的平分线，EF为∠BED的平分线，EF与CD交于点M，CF与BE交于点N．
（1）若∠D=70°，∠BED=30°，则∠EMA=85（度）；
（2）若∠B=60°，∠BCD=40°，则∠ENC=80（度）；
（3）∠F与∠B、∠D有怎样的数量关系？证明你的结论．
15．化简求值：
（1）4（2x2-3x+1）-2（4x2-2x+3）
（2）（2x2y-2xy2）-[（-3x2y2+3x2y）+（3x2y2-3xy2）]，其中x=-1，y=-2．
（3）若xy=4，x-y=$\frac{1}{3}$，求3（xy-$\frac{1}{3}y$）-$\frac{1}{2}$（2x+4xy）-2（-2x+y）
2．先观察下列等式，再回答下列问题：
①$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{1+1}$=1$\frac{1}{2}$；
②$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=1+$\frac{1}{2}$-$\frac{1}{2+1}$=1$\frac{1}{6}$；
③$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=1+$\frac{1}{3}$-$\frac{1}{3+1}$=1$\frac{1}{12}$．
（1）请你根据上面三个等式提供的信息，猜想$\sqrt{1+\frac{1}{{5}^{2}}+\frac{1}{{6}^{2}}}$的结果，并验证；
（2）请你按照上面各等式反映的规律，试写出用含n的式子表示的等式（n为正整数）．
19．据测算，我国一年因土地沙漠化造成的经济损失约为54750000000元，用科学记数法表示这一数据为（　　）万元．
A．5.475×1010B．5.475×107C．5.475×106D．5475×103
20．计算：-32×（-2）+（-2）3-4$÷\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网