题目内容
15.已知抛物线y=2x2-8x+6与x轴相交于点A、B(点A在点B的左边),与y轴交于点C,BC的中点为M,点B关于y轴的对称点为N,则MN的长度等于( )| A. | $\frac{3\sqrt{13}}{2}$ | B. | $\frac{\sqrt{119}}{2}$ | C. | $\frac{\sqrt{110}}{2}$ | D. | 6 |
分析 求出A,B.C的坐标,根据中点公式求出点M坐标,根据对称求出点N坐标,运用两点距离公式即可求解.
解答 解:y=2x2-8x+6,
当x=0时,y=6,
∴点C(0,6),
当y=0时,2x2-8x+6=0,
解得:x=1或x=3,
∴点A(1,0),点B(3,0),
可求BC的中点为M($\frac{3}{2}$,3),点B关于y轴的对称点为N(-3,0),
MN=$\frac{3\sqrt{13}}{2}$.
故选A.
点评 此题主要考查抛物线与x轴的交点问题,会求交点坐标,线段中点坐标,点关于轴的对称点,以及求线段长度是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.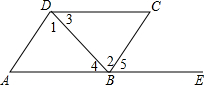 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠A+∠ABC=180° | C. | ∠A=∠5 | D. | ∠3=∠4 |
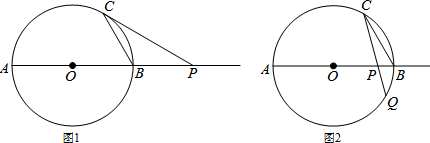
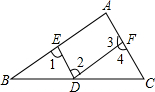 如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )
如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )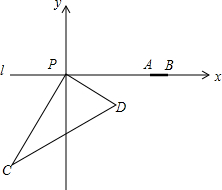 如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.
如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.