题目内容
2．计算题（1）$3\sqrt{3}-\sqrt{8}+\sqrt{2}-\sqrt{27}$
（2）$2\sqrt{12}×\frac{\sqrt{3}}{4}÷5\sqrt{2}$．
分析 （1）先把各个二次根式进行化简，再合并同类二次根式即可；
（2）根据二次根式的乘除混合运算法则计算．
解答 解：（1）$3\sqrt{3}-\sqrt{8}+\sqrt{2}-\sqrt{27}$=3$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{3}$=-$\sqrt{2}$；
（2）$2\sqrt{12}×\frac{\sqrt{3}}{4}÷5\sqrt{2}$=4$\sqrt{3}$×$\frac{\sqrt{3}}{4}$×$\frac{\sqrt{2}}{10}$=$\frac{3\sqrt{2}}{10}$．
点评 本题考查的是二次根式的混合运算，掌握二次根式乘法、除法及加减法运算法则是解题的关键．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
15．已知抛物线y=2x2-8x+6与x轴相交于点A、B（点A在点B的左边），与y轴交于点C，BC的中点为M，点B关于y轴的对称点为N，则MN的长度等于（ ）
| A． | $\frac{3\sqrt{13}}{2}$ | B． | $\frac{\sqrt{119}}{2}$ | C． | $\frac{\sqrt{110}}{2}$ | D． | 6 |
13．在平面直角坐标系中，将点P（a，b）关于原点对称得到点P1，再将点P1向左平移2个单位长度得到点P2，则点P2的坐标是（ ）
| A． | （b-2，-a） | B． | （b+2，-a） | C． | （-a+2，-b） | D． | （-a-2，-b） |
7．
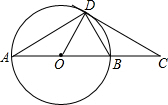如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，DC与AB的延长线交于点C，∠A=30°，给出下面3个结论：∠BDC=∠A；AB=2BC；AD2=3BC2；其中正确结论的个数是（ ）
如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，DC与AB的延长线交于点C，∠A=30°，给出下面3个结论：∠BDC=∠A；AB=2BC；AD2=3BC2；其中正确结论的个数是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
11．方程组$\left\{\begin{array}{l}{x+3y=5}\\{2x-3y=1}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ |
