题目内容
2．|-2|=（ ）| A． | -2 | B． | 2 | C． | ±2 | D． | 4 |
分析 根据绝对值定义去掉这个绝对值的符号．
解答 解：∵-2＜0，
∴|-2|=2．
故选B．
点评 考查了绝对值的知识，解题关键是掌握绝对值的规律．一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．
练习册系列答案
全优点练单元计划系列答案
相关题目
12．
如图，把直尺沿直线断开并错位，点E、D、B、F在同一直线上，若∠ADE=135°，则∠DBC的度数是（ ）
如图，把直尺沿直线断开并错位，点E、D、B、F在同一直线上，若∠ADE=135°，则∠DBC的度数是（ ）| A． | 65° | B． | 55° | C． | 45° | D． | 35° |
10．
如图，点E在AC的延长线上，下列条件不能判断AC∥BD的是（ ）
如图，点E在AC的延长线上，下列条件不能判断AC∥BD的是（ ）| A． | ∠3=∠4 | B． | ∠D=∠DCE | C． | ∠1=∠2 | D． | ∠D+∠ACD=180° |
17．下列计算错误的是（ ）
| A． | 3$\sqrt{3}$+2$\sqrt{2}$=5$\sqrt{5}$ | B． | $\sqrt{8}$÷2=$\sqrt{2}$ | C． | （-$\sqrt{3}$）2=3 | D． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ |
7．
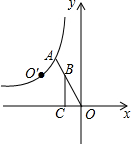如图，点A是双曲线y=-$\frac{2}{x}$（x＜0）上的一点，连结OA，在线段OA上取一点B，作BC⊥x轴于点C，以BC的中点为对称中心，作点O的中心对称点O′，当O′落在这条双曲线上时，$\frac{OA}{OB}$的值为（ ）
如图，点A是双曲线y=-$\frac{2}{x}$（x＜0）上的一点，连结OA，在线段OA上取一点B，作BC⊥x轴于点C，以BC的中点为对称中心，作点O的中心对称点O′，当O′落在这条双曲线上时，$\frac{OA}{OB}$的值为（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{3}{2}$ | D． | $\frac{\sqrt{5}}{2}$ |
14．下列条件不能判定四边形ABCD是平行四边形的是（ ）
| A． | AB∥CD AD∥BC | B． | AB∥CD AB=CD | C． | AD∥BC AB=CD | D． | ∠A=∠C∠B=∠D |
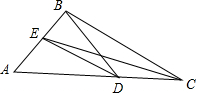已知：在△ABC中，∠ABC=100°，∠C的平分线交AB边于点E，在AC边上取点D，使得∠CBD=20°，连结DE．求∠CED的度数．