题目内容
14．下列条件不能判定四边形ABCD是平行四边形的是（ ）| A． | AB∥CD AD∥BC | B． | AB∥CD AB=CD | C． | AD∥BC AB=CD | D． | ∠A=∠C∠B=∠D |
分析 根据平行四边形的判断定理分别作出判断得出即可．
解答 
解：A、根据平行四边形的判定定理：两组对边分别平行的四边形是平行四边形，故能判断这个四边形是平行四边形，不合题意；
B、根据平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形，故能判断这个四边形是平行四边形，不合题意；
C、不能判断这个四边形是平行四边形，符合题意；
D、根据平行四边形的判定定理：两对角相等的四边形是平行四边形，故能判断这个四边形是平行四边形；
故选：C．
点评 此题主要考查了平行四边形的判定定理，准确无误的掌握定理是解题关键．
练习册系列答案
相关题目
4．《孙子算经》中有一道题：“今有木，不知长短．引绳度之，余绳四尺五，屈绳量之，不足一尺．问木长几何？”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺．”如果设木条长为x尺，绳子长为y尺，根据题意列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{x+4.5=y}\\{\frac{y}{2}+1=x}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=y+4.5}\\{\frac{y}{2}+1=x}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=y+4.5}\\{y=\frac{x}{2}+1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+4.5=y}\\{x=\frac{y}{2}-1}\end{array}\right.$ |
2．|-2|=（ ）
| A． | -2 | B． | 2 | C． | ±2 | D． | 4 |
9．
如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连结EF．若EF=2$\sqrt{3}$，BD=8，则菱形ABCD的周长为（ ）
如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连结EF．若EF=2$\sqrt{3}$，BD=8，则菱形ABCD的周长为（ ）| A． | 8 | B． | 8$\sqrt{6}$ | C． | 16$\sqrt{3}$ | D． | 8$\sqrt{7}$ |
19．
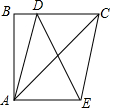如图，在Rt△ABC中，∠ABC=90°，AB=BC=2，点D在BC上，以AC为对角线的所有?ADCE中DE的最小值是（ ）
如图，在Rt△ABC中，∠ABC=90°，AB=BC=2，点D在BC上，以AC为对角线的所有?ADCE中DE的最小值是（ ）| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | $2\sqrt{2}$ |